超々入門相対論 (2) ローレンツ変換

(1)相対性の原理では, 光速度不変の原理と相対性の原理から, 思考実験で時間の遅れや長さの収縮が導けることを示した。しかし, 有名な「ローレンツ変換」を使えば理解はもっと容易になる。しかも, ローレンツ変換は中学高校レベルの数学で簡単に導くことができる。本稿では, 特殊相対論の中核であるローレンツ変換の式を導いてみることにしよう。

ガリレイ変換

ある慣性系 (仮に静止系 O と呼ぼう) と, それに対して\(x\)方向に速度\(v\)で運動する慣性系 (仮に運動系 O' と呼ぼう) を考える。簡単のため, 2つの座標系の原点がちょうど一致していたときの原点での時刻をそれぞれ \(t=0\), \(t'=0\) としよう (図1 参照)。

図のように, 座標系が運動すると見かけの位置が原点の移動分, すなわち \(vt\) だけずれるので, ニュートン力学における運動系の座標と静止系の座標の関係はつぎのようになる。

\[ \begin{align} & x' = x - vt \hfill \\ & t' = t \hfill \\ \end{align} \]

これをガリレイ変換という。このときの座標系 O と座標系 O' の関係を図で表すと図2のようになる。水色 (シアン) が O, 青が O' にあたる。習慣に従って, 時間軸を縦軸としているので, 図の上へいくほど時間が進んでいることになる。座標系のうち, O' が\(x\)方向へ移動しているので, 図のように上へ行くほど\(x'\)が右へずれていくことになる。 O' の速度が大きいほど, ずれかたは大きくなる。図では速度を 0.3 としているが，長さと時間の単位は適当に選んでいるので, この数字に意味はない。また, ニュートン力学では, すべての座標系に共通の絶対時間があると考えるので, 時間は変換を受けない。したがって, 座標の各点が時間軸の方向 (図2の上下方向) にずれることはない。

ところで, ガリレイ変換は残念ながら光速度不変の原理を満たさない。たとえば O 系に対して速度\( c \)で進む光の式 \( x = ct \) をガリレイ変換の式に代入すると

\[ x' = ct - vt = (c - v)t \]

になる。これは, O' から見た光の速度が \( c - v \) になることを意味する。ニュートン力学では, 光はたまたま速度\( c \)で走る粒子にすぎないので, 動きながら光を見るとふつうの粒子の運動と同じように見かけの速度が変化してしまうのだ。ガリレイ変換は修正が必要だ。

ローレンツ変換

ガリレイ変換に代わって光速度不変の原理を満たす変換を考えよう。まず, O' の原点の運動を O から見ると\( x \)方向に速度\( v \)で移動する, すなわち \(x'=0\) のとき \(x=vt\) が成り立つので, \(x'\)の式には \(x - vt\) が含まれるはずだ。また, 2つの座標系が対等であるためには, 式は１次変換 (2次以上の項を含まない) でなければならない。したがって, \(x\)と\(x'\)との間にはつぎのような関係が成り立つと考えられる。

\[ x' = A(x - vt) \tag{1} \]

ここで\(A\)は係数だ。この係数が 1 だとニュートン力学になってしまうので, 相対論では 1 以外の値になるはずだ。ところで, 相対性の原理から慣性系は対等なので, O' 系から見ると O 系の原点は \( -v \) で移動するように見える。すなわち, つぎの関係も同時に成り立つはずだ。

\[ x = A(x' + vt') \tag{2} \]

けっきょく係数\(A\)を求める問題になった。 \(A\)は光速度不変の原理から求めることができる。すなわち, 同じ光が O 系から見ても O' 系から見ても速度\(c\)で走るので, 時刻 0 に原点を出発した光に対してつぎの式が成り立つ。

\[ x = ct \tag{3} \]

\[ x' = ct' \tag{4} \]

これで4つの式が揃った。これらの式から \(x\), \(x'\), \(t\), \(t'\) の4つを消去すれば, 残る\(A\)が求められるはずだ。

\[ ct' = A(c - v)t \tag{1'} \]

\[ ct = A(c + v)t' \tag{2'} \]

\[ {c^2}t = {A^2}(c + v)(c - v)t \]

\[ {c^2}t = {A^2}({c^2} - {v^2})t \]

\[ {A^2} = \frac{{c^2}}{{c^2} - {v^2}} = \frac{1}{{1 - \tfrac{{v^2}}{{c^2}}}} \]

\[ x' = \frac{{x - vt}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }} \tag{5} \]

\(t'\)の式は, (1) 式と (2) 式から\(x'\)を消去すると出てくる (計算省略)。すなわち,

\[ t' = \frac{{t - \tfrac{v}{{c^2}}x}}{{\sqrt {1 - \tfrac{{v^2}}{{c^2}}} }} \tag{6} \]

この (5), (6) が有名なローレンツ変換^[1]だ。

[1] ローレンツ変換の式 (5), (6) では省略したが, 進行方向に垂直な方向の座標は不変だ。すなわち,
\[ \begin{align} & y' = y \hfill \\ & z' = z \hfill \\ \end{align} \]
これは, 2つの座標系が対等であることから理解できる。もし変換を受けて一方の座標の長さが仮に縮小するなら, 立場を入れ替えたもう一方の長さも縮小するはずだ。座標系が対等で互いに長さが縮小されるとすれば, 縮小率は 1 でなければならない。つまり, 進行方向に垂直な方向の長さは変化しないことがわかる。

このままでは, 2つの式は形がすこし異なるので, あまり美しくない。これは一方が長さの式, もう一方が時間の式であるためだ。時間に光速度をかけて長さの単位に揃えておくと, ローレンツ変換の式は \( x \) と \( ct \) について対称になる。すなわち,

\[ x' = \frac{{x - \tfrac{v}{c}ct}}{{\sqrt {1 - \tfrac{{v^2}}{{c^2}}} }} \tag{5'} \]

\[ ct' = \frac{{ct - \tfrac{v}{c}x}}{{\sqrt {1 - \tfrac{{v^2}}{{c^2}}} }} \tag{6'} \]

ところで, 係数\(A\)の代わりに記号\( \gamma \) (ローレンツ因子という) がしばしば使われる。すなわち \( \gamma = 1 / \sqrt {1 - {\textstyle{{{v^2}} \over {{c^2}}}}} \)。また \( \beta = v / c \) という記号がよく使われる。これらの記号を用いると, ローレンツ変換は

\[ x' = \gamma (x - \beta ct) \tag{5''} \]

\[ ct' = \gamma (ct - \beta x) \tag{6''} \]

のように \( x \) と \( ct \) について対称でコンパクトな式で表すことができる。

ここで, ローレンツ変換とガリレイ変換のあいだの関係について見てみよう。ローレンツ変換の式 (5), (6) で \(v/c \to 0\) の極限を考えると, 式 (5) は \(x' = x-vt\) に, 式 (6) は \(t' = t\) になることがわかる。すなわち, 速度\( v \)が光速度\(c\)に比べて十分遅いときには, ローレンツ変換はガリレイ変換に移行するのだ。ローレンツ変換は, 速度が小さい極限としてガリレイ変換を含んでいるというわけだ。

時空図で表したローレンツ変換

ローレンツ変換を座標の図で表すと, 時間の遅れや長さの収縮を図で理解することができる。時空図を描くときは, 習慣で時間軸を縦にとることになっている。また, 時間の単位を長さに換算するために, 光の速度を掛けて \(ct\) としている。したがって, 1 光秒 (約 3×10⁸ m) の長さが 1 秒の時間に対応する。


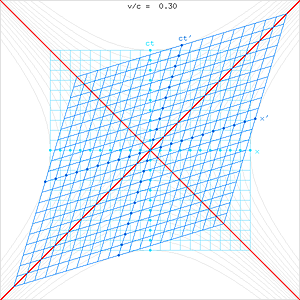
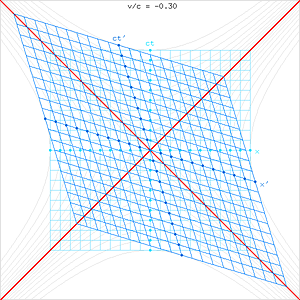
図3a. 空間を横軸に, 時間を縦軸にしたときの, ローレンツ変換の時空図。 \(v > 0\) のとき。動画を止め, スライダーで \(v/c\) の値を調整して見てほしい。		図3b. 空間を横軸に, 時間を縦軸にしたときの, ローレンツ変換の時空図。 \(v < 0\) のとき。

図3は, O' の\(x\)方向の移動速度\(v\)をいろいろな値に変化させたときのローレンツ変換を, 時空図で表したものだ。ガリレイ変換のときは, 時間が変換を受けないため, \(ct\) 軸だけが傾いて, \(x\)軸は傾かないが, ローレンツ変換では\(x\)軸も変換を受けて傾くのが特徴だ。これは, いっぽうの座標では同時である時間が, 座標が運動すると場所によって少しずつずれるためだ。

ローレンツ変換の時空図 (図3) で, 赤い線は光の経路を表す。図を見るとわかるように, \(x\)軸と\(ct\)軸はローレンツ変換によって互いに接近し, 速度が光速度に近づくにつれて座標軸はともに光の経路に近づいていく。このとき, 長さや時間の目盛は, 双曲線 (細い破線) に沿って移動することに注意してほしい。その結果, 時空図の格子 (正方形または平行四辺形) の面積は一定に保たれる。これは, 平面の回転変換とちょっと似ている。回転変換では, 2つの軸は同じ向きに回転するので互いに接近することはなく, 長さの目盛も円に沿って動くところがローレンツ変換と異なるが, 格子の面積が一定に保たれるところはローレンツ変換と同じだ。

図4. 空間を横軸に, 時間を縦軸にしたときの, ローレンツ変換の時空図。青い軸は, O 系に対して速度\(v\)で運動する列車の座標軸を表す。

図4は, 速度\(v\)で運動する列車の時空図だ。図4の中で, 青で示した座標軸が列車といっしょに動く座標軸を表す。座標の移動に伴って, 時間軸 (\(x' = 0\)の軸) が傾くだけでなく空間軸 (\(ct' = 0\)の軸) も傾くことがわかる。これは, 運動する座標系での同時が, 静止系では場所によって別々の時刻になるためだ。軸に沿って入れた目盛は単位長さを表す。図をよく見ると, 長さや時間の目盛の間隔が座標系によって異なっている。ローレンツ変換の時空図では, 長さや時間の目盛が双曲線 (破線) に沿って一定になることに注意してほしい。

図4の中で, 赤い線は正方向と負方向に運動する光を表す。また, 薄青色の帯は, 移動する列車を表す。この薄青の帯を, 静止系における同時で切り取ったもの (灰黄色の細長い長方形) が, 静止系で見た列車だ。また, 青い帯を列車における同時で切り取ったもの (青色の細長い平行四辺形) が, 列車の座標系で見た列車だ。このように, 列車の長さを見るためには, 観測する座標系での「同時」における列車の前後の位置の差を見ないといけない。図中の赤い星★は, 列車の真ん中を出発した光が列車の後端と前端に着く時刻と場所を表す。列車の中の時間では同時だが, 列車の外の時間では先に後端に着き, ずいぶん遅れて前端に着くことがわかる。

図の列車の長さを見ると, 静止系で見た列車（灰黄色）の長さが, 本来の長さ (1 から −1 まで) よりも短いことがわかる。このように, 運動するものの長さはつねに進行方向に短くなる。これがローレンツ収縮だ。

つぎに時間の遅れを見てみよう。例えば列車の中央に置かれた青い時計に注目しよう。この時計を外から時刻 1 (\(ct = 1\)) に見ると, 列車の中央の青い時計はまだ時刻 1 にはなっていないことがわかる ( \(v/c = 0.6\) の場合, 計算すると列車中央の時刻は 0.8)。同じように, 地上の原点に置いてある黄色い時計を, 列車の中から時刻 1 (\(ct' = 1\)) に見ると, 地上の黄色い時計はまだ時刻 0.8 で, 時刻 1 にはなっていないことがわかる。このように, 動いている時計の時間, あるいは運動している座標上の特定の点における時間は必ず遅れるのだ。

時間の遅れと長さの収縮

ここでは, ローレンツ変換の図ではなく式を使って時間の遅れと長さの収縮を導いてみよう。まず, ローレンツ変換の式はつぎのようなものであった。

\[ x' = \frac{{x - vt}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }} \tag{5} \]

\[ t' = \frac{{t - \tfrac{v}{{c^2}}x}}{{\sqrt {1 - \tfrac{{v^2}}{{c^2}}} }} \tag{6} \]

これらを\(x\)と\(t\)について解くと, 逆変換の式はつぎのようになる。

\[ x = \frac{{x' + vt'}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }} \tag{7} \]

\[ t = \frac{{t' + \tfrac{v}{{c^2}}x'}}{{\sqrt {1 - \tfrac{{v^2}}{{c^2}}} }} \tag{8} \]

いま, O' 系の原点 \(x' = 0\) に置かれた時計の示す時間を \({t_0}\) としよう。この時間は, 時計本来の時間なので固有時ということがある。これを静止系からみた時間は, (7) に \(x' = 0\) と \(t' = {t_0}\) を代入すると得られる。すなわち,

\[ t = \frac{{t_0}}{{\sqrt {1 - \tfrac{{v^2}}{{c^2}}} }} \]

あるいは,

\[ {t_0} = \sqrt {1 - \tfrac{{v^2}}{{c^2}}} \,t \]

これは, 動いている時計の時間がゆっくりと進むことを表す。

つぎに，O' 系に置いた\(x\)方向の長さが \({L_0}\) のものさしを考える。これは, ものさし本来の長さなので固有長ということがある。いま, ものさしの前端を \(x' = {L_0}\), ものさしの後端を \(x' = 0\) とする。 O 系でのものさしの前端の運動は, (5) 式に \(x' = {L_0}\) を代入し\(x\)について解くと得られる。すなわち,

\[ x = \sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} \,{L_0} + vt \tag{9} \]

同様に, O 系でのものさしの後端の運動は, (5) 式に \(x' = 0\) を代入し\(x\)について解くと得られる。すなわち,

\[ x = vt \tag{10} \]

O 系でのものさしの前端と後端の差 (9) − (10) を計算し, これを\(L\)とすると，

\[ L = \sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} \,{L_0} \]

これは, 動いているものの長さが進行方向に収縮することを表す。

速度の合成則

ローレンツ変換を使って, 速度の足し算の式を導いてみよう。いま, 速度\(u\)で\(x\)方向に移動する質点を考える。これを, 速度\(v\)で\(x\)の負方向に移動する運動系から見ると, 合成速度\(V\)はニュートン力学では \(V = u + v\) となる。これでは, 光速度に近い速度どうしを足すと, 合成速度が光速度\(c\)を超えてしまう。相対論での正しい合成速度を求めてみよう。

図5. 速度\(u\)で動く質点を, 逆向きに速度\(v\)で動く座標系から見ると, 合成速度はどうなるのだろう。

まず, 静止系と, 負方向に速度\(v\)で移動する運動系の間のローレンツ変換の式を挙げておこう。これは, ローレンツ変換の式で速度\(v\)を\(-v\) に置き換えるだけで得られる。すなわち,

\[ x' = \frac{{x + vt}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }} \]

\[ t' = \frac{{t + \tfrac{v}{{{c^2}}}x}}{{\sqrt {1 - \tfrac{{v^2}}{{c^2}}} }} \]

いっぽう, 速度\(u\)で運動する質点に対してつぎの式が成り立つ。

\[ x = ut \]

これを上のローレンツ変換の式に代入すると,

\[ x' = \frac{{ut + vt}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }} = \frac{{u + v}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }}t \]

\[ t' = \frac{{t + \tfrac{v}{{{c^2}}}ut}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }} = \frac{{1 + \tfrac{{uv}}{{{c^2}}}}}{{\sqrt {1 - \tfrac{{{v^2}}}{{{c^2}}}} }}t \]

これより, 運動系から見た質点の合成速度\(V\)を求めることができる。すなわち,

\[ V = \frac{{x'}}{{t'}} = \frac{{u + v}}{{1 + \tfrac{{uv}}{{c^2}}}} \]

これが, 相対論における速度の合成則だ。たとえば, この式を使って光速度の 1/2 倍どうしを足した速度を計算すると光速度の 4/5 倍になる。このように, 2つの速度が光速度に近いと合成速度も光速度に近くなるが, けっして光速度を超えることはない。また, 速度の一方を光速度\(c\)にすると, 合成速度は\(c\)になる。速度の合成則が光速度不変の原理をちゃんと満たしていることがわかる。

付録 ― ローレンツ変換と回転変換

戻る
T. Fujiwara, updated 2024/09