3次元 CG は,コンピュータによってリアルな画像を作る技術である。
静止画だけでなく,CM,アニメーション,映画(実写との合成を含む)など多くの分野で使われている。
3次元 CG を作るためには,オブジェクトの形状の作成(モデリング)・質感(アトリビュート)の調整,照明・視点(カメラアングル)の調整など,たくさんのことを行わなければならない。
動画を作成するためには,さらに,モーションデザイン,カメラワークも必要である。また,多数のコマを作成するため,多くの計算時間も必要である。
3次元 CG は,映像をつくる過程(レンダリング)に多くの計算を必要とするため,かつては高価なコンピュータが必要であったが,
コンピュータの処理能力が向上したため,最近ではパソコン (ただしハイスペックのもの) がふつうに使われる。
* ここでいう3次元は,3D 映画 (ステレオ映画) や 3D 放送の意味で使われる,両眼視による 3D 映像ではなく,広く CG (立体のコンピュータによる映像化) の意味で使われる3次元である。 単に CG と呼んでもよい。
モデリングでは,座標上で立体・光源・カメラを配置するので,3次元座標についての知識が必要になる。座標軸 x y zの取り方はソフトウェアによって若干異なる。
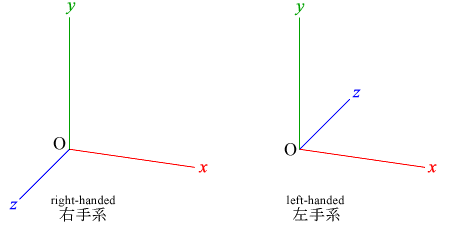
親指にx軸,人差指にy軸,中指にz軸を当てた場合,右手の配置になるものを右手系,左手の配置になるものを左手系という。 数学では右手系が使われるが,3次元 CG ではソフトウェアによって右手系のものと左手系のものがある(右手系が多いようだ)ので,どちらが使われているか注意する必要がある。 図のように,右手系では手前が z 方向に,左手系では奥行きが z 方向になる。

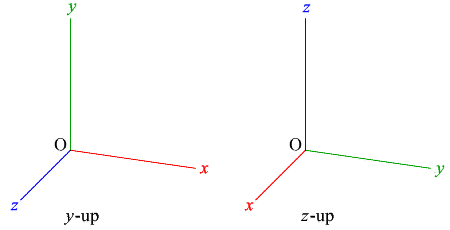
y軸が上を向く座標の取り方を y-up,z軸が上を向く座標のとり方を z-up という。
3次元CGでは画面上の右を x, 上を y にとるのがふつうなので y-up となる。
したがって,右手系では z 軸が手前側,左手系では z 軸が向こう側になる。
いっぽう,CAD(製図ソフト)では平面図を x-y 面とするのがふつうなので z-up となることが多い。数学でも z-up の右手系が使われる。
ちなみに,主要な3次元 CG ソフトウェアでは Maya, SoftImage (XSI), Houdini, Shade が右手系 y-up, LightWave が左手系 y-up, Rhinoceros が右手系 z-up のようだ。
CG では,形状を座標 (x, y, z) で表現する。 座標は単なる数値のままで扱い,いちいち単位を付けて表すわけではないが,ソフトウェアごとに単位が仮定されている。 単位は mm か cm であることが多い。 CG のアニメーションで重力による落下などの物理現象を扱う場合は,仮定されている単位を把握しておかないと非現実的な速度の運動になってしまうので注意が必要である。
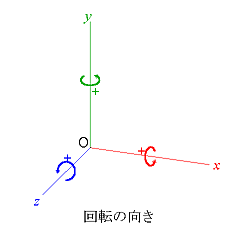
物体を回転するときは,回転軸と角度を指定しなければならない。角度は,xyz サイクリックの順をプラスにするのがふつうの定義である。すなわち, x軸のまわりの回転では y→z の向きがプラスに,y軸のまわりの回転では z→x の向きがプラスに,z軸のまわりの回転では x→y の向きがプラスになる。
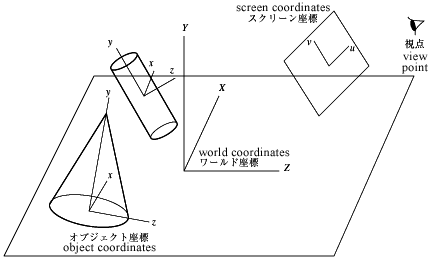
モデリングを行うときは,まず物体を作り,それを回転・平行移動させて配置していく。 物体作成に使った座標をオブジェクト座標という。 また,物体・光源・カメラを配置する舞台となる座標をワールド座標という。 これを,カメラの位置から見ると透視図が得られるが,これがレンダリングで得られる画像で,画像上での座標がスクリーン座標である。
大別して,つぎの2つの立体表現がある。どれが使われるかはソフトウェアによる。
ポリゴン(polygon, 多角形のこと)による面素の集まりでできた,中身のない表面だけのモデル。おもに Z バッファ法,スキャンライン法で使われる。 モデリングにはつぎのような方法が使われる。
表面だけのサーフェスモデルに対して,中身の詰まったモデルをソリッドモデルという。主としてレイトレーシングに使われる。面素でできたB-reps(Boundary representation, 境界表現)と,プリミティブを組み合わせる方法がある。
実際にモデリングを行うときは,以上のような方法で立体を作り,スケール変換(拡大・縮小)で大きさを整え,回転や平行移動で配置を決めていく。また,いくつかの立体を適当にまとめてグループ化する(例えば指と手のひらをまとめて「手」として扱う)と,モデリングが容易になる。

|
|

|

|
| 回転体 (ワイアフレーム 表示) |
ポリゴンでできた プリミティブの 組み合わせ |
濃度球の例 (LINKS メタボール) |
CSGの例 球から直方体を 切り取っている |
上記の形状データのうち,ポリゴンで表現された形状を保存する汎用のファイル形式として,DXF や STL がある。 いずれも各ポリゴンの座標値と法線 (面の向き) 情報の集合である。 DXF (Drawing Exchange Format) は AutoDesk 社による汎用の 2D/3D データの保存形式で,CAD 方面で使われる。 STL (STereo Lithography または Standard Triangulated Language) は,形状を三角形の面素で表したもので,3D プリンタ用のデータとして使われることが多い。