"Solar System Dynamics"

Murray and Dermott's "Solar System Dynamics" (1999), a famous British textbook on solar system dynamics, makes the mistake of calling translational inertial forces "centrifugal forces of equal magnitude and direction". It seems that many planetary science students are studying with this textbook, so please be careful about this mistake. This force cannot be a centrifugal force because the planet is moving in a translational circular motion and not rotating. All references to centrifugal force in p. 132 must be rewritten as inertial force.
* Rotation refers to the motion of a rigid body going around a rotation axis while changing its orientation. On the other hand, translational circular motion is the motion of a rigid body going around without changing its orientation. For a rigid body, rotational motion and translational motion are different, and should not be confused.

You should also be cautious with the explanation that divides the translational circular motion of the planet into the circular motion of each point, as shown in the figure on p. 132 (below). In the motion of a point mass, circular motion is usually treated as rotational motion. However, for rigid bodies, you must distinguish between translational and rotational motions. The description of Fig. 4.2 says that all points have circular motion with equal radii but different centers. This merely explains that the motion of the planets is translational motion along the circle. The problem is what comes next. As can be seen from the text, the inertial force appearing due to this circular motion of each point is incorrectly called "the same centrifugal force everywhere." This is probably because the circular motion of each point is mistaken for rotational motion. In truth, the motion is the translational circular motion of the reference frame fixed to the rigid body, not the rotational motion of the individual frames around their respective centers; in the first place, for a rigid body, there cannot be such rotational motion with multiple axes of rotation. Since the motion is just translational accelerated motion, the force which appears on the rigid body is the usual uniform inertial force (translational inertial force). Of course, the inertial forces are the same everywhere, because all points have the same motion.

If translational circular motion is divided into circular motion of each point in this way, there is a risk of misunderstanding it as rotational motion (in fact, many people do misunderstand it that way...). If we consider forces acting on a rigid body, we should consider "force field" acting on the reference frame of the rigid body, instead of dividing the rigid body into individual points. Therefore, it would be important to emphasize that the revolution of a planet without rotation is the translational accelerated motion of a rigid body, rather than dividing the motion of a planet into a circular motion of each point.

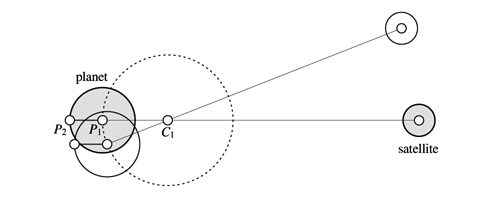Fig. 4.2. (proposed) A figure like this is sufficient to show that the motion of the planet is translational. To avoid mistaking circular motion for rotational motion, it is better not to draw unnecessary circles.

Solar System Dynamics - Amendments