 |
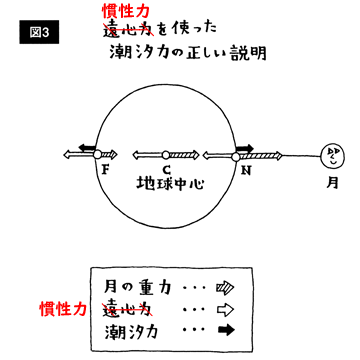
| 「間違いだらけの物理学」 4章 図3。 学校の教科書の表現に合わせて「遠心力」と書いているが, 正しく「慣性力」と書くべきだろう。 |
「間違いだらけの物理学」(2014)
松田卓也氏といえば, 疑似科学を鋭く斬ることなどで知られているが, この「間違いだらけの物理学」も, おそらく多くの人が陥っていると思われる物理の誤解をわかりやすく訂正している痛快な本だ。 専門的な内容にまで踏み込んで書いてあるので, 物理教育に関わっている人や研究者向けの本かもしれない。 この本では, 第3章が「遠心力」, それに続いて第4章が「潮汐力の説明」の話題に当てられているが, 第4章はちょっと切れ味が悪いように思える。 というのは, 遠心力ではない力 (一様慣性力, あるいは並進慣性力) を「遠心力の一部の成分」という曖昧な名称で呼んでいるからだ。 本稿の本文で書いたように, この一様な力は遠心力とは別の力なので「遠心力」と呼んではいけない。 一部の成分とはいえ, 「遠心力」という言葉を使うかぎり潮汐力の説明の混乱は解消しないだろう。 ここでは, 松田氏の用語の使い方を少し修正してみよう。
潮汐力は, 大きさを持つものが天体から重力を受けるだけで現れる力で, 原因は重力の非一様性だ。 地球の各点の重力と地球の中心での重力の差を取るだけで出てくる。 中心での重力との差を取る代わりに, 中心での重力とは逆の力すなわち一様な慣性力との合力を求めてもよい。 高校の教科書では, 地球の自転による影響が出ないよう, 地球が地球-月の共通重心の周りを自転のない公転運動をしているとして, 並進加速度運動する地球に現れる一様な慣性力を使って潮汐力を説明する。 この一様な慣性力は並進運動によって現れる慣性力なので, 慣性力 (見かけの力) 全般と区別するために並進慣性力と呼ぶことがある。 地球は回転運動 (向きを変える運動) をしていないので, この慣性力は遠心力ではありえない。 教科書は, この並進慣性力を誤って大きさと向きが同じ「遠心力」と呼んでいるわけで, これは遠心力の誤用だ。
松田氏は, まず教科書に出てくる説明図 (図3) を話題にして, この説明図は正しいというところから話を始める。 図はたしかに正しいが, 上述のように教科書は並進慣性力のことを間違って遠心力と呼んでいる。 この慣性力を教科書と同様に遠心力と書いてしまうと誤用を追認することになるので, 正しく慣性力と書くべきだ。 あるいは, 少なくとも「×遠心力」や「遠心力??」のように書いて誤用であることを示すべきだろう。
 |
| 「間違いだらけの物理学」 4章 図3。 学校の教科書の表現に合わせて「遠心力」と書いているが, 正しく「慣性力」と書くべきだろう。 |
松田氏は, 教科書のような, 自転のない公転だけの運動で潮汐力を説明するというアプローチを使わず, 本稿本文の「回転系で見た潮汐力」と同様に, 公転運動とともに回転する回転系に乗って潮汐力を説明する。 並進加速度系ではなく回転系に乗るのは, そのほうが月も地球も止まって見えるので話が簡単になるからだ。 この, 共通重心を中心とする回転系に乗ると遠心力 (こんどは本物) が現れる。 遠心力は, 高校の物理で習うように回転軸からの距離に比例して外向きにはたらく力なので, 遠心力と月による重力との合力を図に描くと 図5 のように潮汐力よりもずっと大きい力になる。 ところで松田氏は, 月に近い側と遠い側で合力の大きさが同じにならないと書いているが, ちゃんと計算すれば (あるいは矢印を正しく描けば) 近似の範囲で大きさは等しくなるはずだ。 下の図では, 矢印の長さを正しく描き直しておいた。
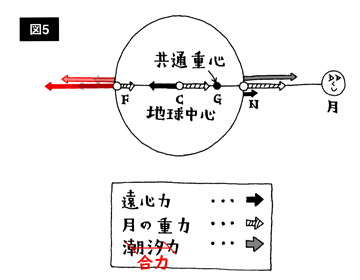 |
| 「間違いだらけの物理学」 4章 図5。 遠心力と月の重力の合力は, 月に近い側と遠い側で同じ大きさになるはずだ。 もとの図 (グレイ) では月から遠い側の遠心力が小さすぎたので, 赤で描き直しておいた。 この合力は潮汐力ではないので, 「潮汐力」と書かない方がよい。 |
さて, 回転系に乗ると現れる共通重心中心の遠心力は, 本稿本文の「回転系で見た潮汐力」と同様にして, 地球中心の遠心力と並進慣性力に分けることができる。 一般に回転系では, 回転軸を剛体のどこに取るかは自由で, 回転軸の位置を移動するとその差は並進運動になる。 このことは, 有名なランダウ=リフシッツの「力学」にも書いてある。 これを地球-月系に適用すると, 回転軸を共通重心から地球の中心へ移動することで, 並進運動に伴う一様な慣性力が現れるということになる。 いっぽう, 地球中心の遠心力は白道面に沿ってどの向きにも同じ大きさではたらくので, 潮汐には寄与しない。 図11 は, 地球中心の遠心力を無視して, 一様な慣性力と月の重力だけを描いたものだ。 このように, 回転系で考えても 図3 と同じ図を描くことができる。 しかも, 並進運動のときと違って, こんどは月が動かない。 松田氏は, この慣性力を「遠心力の一部の成分」と書いているが, 遠心力と呼んでもよいという誤解を与えるので, ちゃんと「(並進) 慣性力」と書くべきだろう。 じっさい, 並進慣性力の場は一様であって, 大きさが場所によって変わる遠心力の場とは異なる。
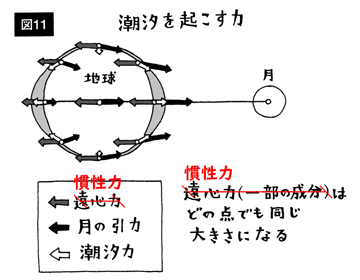 |
| 「間違いだらけの物理学」 4章 図11。 一様な慣性力 (並進慣性力) を, 遠心力の一部の成分として出てくるからといって「遠心力」と呼んではならない。 |
以上のように, 4章の記述の歯切れが悪いのは, 遠心力ではない力 (一様な慣性力) を遠心力の一部の成分という紛らわしい名前で呼んでいるからだろう。 ここは, はっきりと区別して (並進) 慣性力と書くべきだ。 なぜなら, 並進慣性力と遠心力は別の力であって, 力の場も並進慣性力と遠心力では全く異なるからだ。