SIR モデルによる感染症流行シミュレーションを Excel で

新型コロナウイルス SARS-CoV-2 による感染症が拡大して 100 年に一度という事態に発展している。感染症対策専門家会議が招集されて, 政府の方針決定に対する助言を行っているようである。ところが, その会議が発表する資料はあまり科学的ではなく, 判断のための根拠がほとんど示されないだけでなく, 説明も不十分であるように思える。さらに困ったことに, 資料のグラフやデータに誤りがあったりする。牧野氏が公開日誌でいろいろ問題点を指摘しているので, 専門家会議のメンバーも報道関係者もしっかりと読んで勉強してもらいたいものだ。

ところで, 報道でよく見かける予測グラフは, 感染拡大の SIR モデルという数理モデルを使って計算されたものが多い。この SIR モデルは, 単純なわりには大まかな振る舞いが予測できる便利なものである。しかも, 式は理系の人なら簡単に解くことができるもので, 指数関数さえ理解できれば Excel でグラフを描くこともできる。ここでは, SIR モデルを解説し, 予測グラフを描くための式と, シミュレーションの例を紹介しよう。ちなみに, 筆者は天文屋である。

SIR モデル

Kermack and McKendrick の SIR モデルでは, 未感染の人 (Susceptible) の数を \( S \), 感染中の人 (Infected) の数を \( I \), 回復した人 (Recovered) の数を \( R \), 考える集団の人口を \( N \) (一定) として, これらがつぎの常微分方程式で記述できるとする。係数の定義にはいくつかの流儀があるが, ここでは Wikipedia (英語版) に準じた。

\[ \begin{align*} & S + I + R = N{\rm{(const.)}}, \tag{1} \\ & \frac{dI}{dt} = \beta \frac{SI}{N} - \gamma I , \tag{2} \\ & \frac{dR}{dt} = \gamma I . \tag{3} \end{align*} \]

ここで \( \gamma \) は感染した人の回復の速さ (回復率) で, 平均回復時間の逆数で定義され, 単位は時間の逆数になる。時間の単位を日とすると, 1日あたり感染者のうちどれくらいの割合の人が回復するかを表す。また \( \beta \) は感染が広がる速さ (感染者増加率) で, 1人の感染者が1日あたり何人にうつすかを表す。

この式では, 簡単化のためつぎのようなことが仮定されている。

ところで, 感染者の増加率 \( \beta \) の代わりに, これを感染者の回復率 \( \gamma \) で割った \( R_0 = \beta/\gamma \) を使うことが多い。 \( R_0 \) は, 基本再生産数と呼ばれる量で, 報道にもよく出てくる。対策前の再生産数を基本再生産数, 対策後の再生産数を実効再生産数と呼んで区別することがある。 1人の感染者が回復するまでのあいだに平均で何人に感染させるかを表す数で, これが 1 より大きいか小さいかで感染拡大のようすが変わるという, 感染状況の理解にとって重要な量だ。この\( R_0 \) を使うと, 式はつぎのようになる。

\[ \begin{align*} & \frac{dI}{dt} = R_0 \gamma \frac{SI}{N} - \gamma I , \tag{4} \\ & \frac{dR}{dt} = \gamma I . \tag{5} \end{align*} \]

さらに式を, 感染者数, 回復者数そのものではなく, それぞれの全体に対する割合 \( x = I/N \), \( y = R/N \) を使って書き換えると, つぎのような見通しのよい式になる。

\[ \begin{align*} & \frac{dx}{dt} = R_0 \gamma (1 - x - y) x - \gamma x , \tag{6} \\ & \frac{dy}{dt} = \gamma x . \tag{7} \end{align*} \]

集団の大多数がまだ感染していないとき, すなわち \( x, y \) が 1 よりもずっと小さいときは, 式がさらに簡単になる。

\[ \begin{align*} & \frac{dx}{dt} = (R_0 - 1) \gamma x , \tag{8} \\ & \frac{dy}{dt} = \gamma x . \tag{9} \end{align*} \]

2020年5月現在, 感染が広がっている国でも感染者の割合は 0.001 の桁なので, この簡単な式が成り立つ段階である。微分方程式 (8), (9) は容易に解けて, 解が指数関数で表せるので, あとで示そう。

SIR モデルによるシミュレーション

上のグラフのうち赤色の曲線は, 2月から3月ごろ, \( R_0 \)が大きいと感染者が急増して医療崩壊を起こすので \( R_0 \)を 1 に近づけてピークを低くし医療崩壊を防ごう, という説明によく使われた図なので見たことがある人も多いだろう。これを見て, パンデミックは自然に収束するものだと思った人がいるかもしれない。しかし図の縦軸 (人口に対する割合) や横軸 (日) を見てわかるように, この図は何年もかけて人口の何割もの人が感染して集団免疫を付けることで感染を抑えるという, 100年前のスペイン風邪と同じような経過をたどるときの図だ。 \( R_0 \) が 1.2 でも人口の約3割が感染するという, 医療崩壊どころか何十万人もの死者が出るシナリオの図だ。こんな作戦は許されるべきではない。あくまで再生産数を 1 よりも小さくして感染拡大を抑えつづける (おそらくワクチンや効果的な治療薬が出回るまで) という作戦をとるべきだろう。

パラメータの推定

ところで, 感染拡大の予測をするときに重要なのが \( \gamma \) と \( R_0 \) の数値だ。まず回復の速さを表す \( \gamma \) であるが, これは平均回復時間の逆数で見積もることができる。新型コロナウイルス感染症は治りが悪く回復に20～30日もかかるようだ。もし平均回復時間が20日だとすると \( \gamma \) は 0.05, 30 日だとすると約0.03と見積もることができる。 \( \gamma \) は, 1日あたりの感染者の回復率のことなので, 感染中の感染者数に対して1日あたりその何%の人が回復しているかで推定することもできる。感染拡大が収まって落ち着き始めている韓国, イタリア, スペイン, ドイツなどの4月のデータを元に計算してみると, 国によって 0.03 (3%) から 0.06 (6%) とばらつきがあるが, 平均は 0.04 程度であった。ここでは, \( \gamma = 0.04 \) を採用することにしよう。これは, ウイルスの性質によって決まる数値なので, 時間的に変動するものではない。もし感染者のほとんどを早期発見し隔離することができたら実質的な回復時間が短くなる (\( \gamma \) が大きくなる) という効果はあるが, 未発見の感染者が多いような状況の国ではその効果はあまりないだろう。

もうひとつの基本再生産数 \( R_0 \) であるが, 指数関数的に増大しているとき, 感染者数あるいは累計感染者数の増加率は後述するように \( (R_0 - 1) \gamma \) と表せるので, これと感染状況との比較から推定することができる。たとえば 1 日あたり 6% の割合で増えていると, \( (R_0 - 1) \gamma = 0.06 \) ということであり, 先ほどの \( \gamma = 0.04 \) を使えば \( R_0 = 2.5 \) と見積もることができる。ちなみに 1日あたりの増加率 0.06 の逆数は平均増加時間 (\( e = 2.71828 \) 倍になる時間) を表す。この平均増加時間に 0.7 を掛けると倍加時間になる。つまり倍加時間は 0.7/0.06 = 約 12 日ということだ。倍加時間の式は公式として覚えておくとよいだろう。 0.7 は 2 の自然対数の近似値。
公式：倍加時間(日) = 0.7 ÷ (1日あたりの増加率)

図3は国内の累計感染者数のグラフであるが, そこに増加率 \( (R_0 - 1) \gamma \) を表す直線を加えておいた。増加率は時期によって変動している。 3月～4月上旬で合わせると増加率 0.08, \( R_0 = 3.0 \) となる。非常事態宣言が出たころの4月中旬で合わせると増加率 0.06, \( R_0 = 2.5 \) だ。 3.0 のほうが合っているような気がするが, ここでは報道でよく出てくる \( R_0 = 2.5 \) を採用することにしよう。 PCR検査の件数が少ないので隠れ感染者が何倍もいるのでは？という問題は残る。この方法が使えるのは, 全感染者のうち見つかる割合がつねに一定であるときだけだ。もし感染が拡大して発見率が落ちたとすれば, 全感染者の増え方はもっと大きいはずなので本当の再生産数は大きくなる。

ところで, 感染者数の増加率から再生産数を求めるときには回復率 \( \gamma \) の値が必要だ。この値が大きすぎると, 再生産数が小さめに出てくるので, 対策がうまくいっていると判断してしまう可能性がある。専門家会議は \( \gamma \) の値について明らかにしていないが, 専門家会議提言(5/1) の図3に示されている実効再生産数の推定値と下図との比較 (あるいは下図の元データから後述の式 (13) を使って求めた値との比較) から, 専門家会議は \( \gamma \) の値を 0.06 かそれ以上として計算しているのではないかと思われる。ちょっと大きすぎるのではないだろうか。

式でシミュレーション

大多数がまだ感染していないという状況では, 簡単な式 (8), (9) が使える。理系の大学生なら容易に解けるはずで, 解は指数関数になる。 (指数関数そのものは, 高校の理数系の課程で習う。)
まず, 式 (8) の解は

\[ x = x_0 e^{({R_0} - 1)\gamma t} . \tag{10} \]

ここで \( x \) は (感染中の) 感染者の割合を, \( x_0 \) は初期値を表す。 \( R_0 > 1 \) のときは指数関数的に増加する解に, \( R_0 < 1 \) のときは指数関数的に減少する解になっている。 \( R_0 = 1 \) のときは感染中の感染者数は一定になる。これは, 感染者増加率と回復率がちょうどつり合うためである。

\[ y = \frac{x_0}{R_0 - 1} e^{(R_0 - 1)\gamma t} + C . \]

これは回復者の割合を表す。 \( C \) は積分定数で, 初期条件に応じて決まる。
\( R_0 > 1 \) の指数関数的増加のときは, 積分定数がちょうど 0 になるように初期条件を選ぶと便利だ。回復者数は時間とともに極端に大きくなって初期条件の影響がほとんどなくなるので, 初期条件を適当に選ぶことは正当化できる。こうして得られる解はつぎのような簡単な式になり, \( x \) との比が \( y/x = 1/(R_0 - 1) \) と一定になっている。

\[ y = \frac{x_0}{R_0 - 1} e^{(R_0 - 1)\gamma t} . \tag{11} \]

\( R_0 < 1 \) のときは, 時間 \( t = 0 \) で \( y = y_0 \) という初期値になるように積分定数を決めるとつぎのような解になる。

\[ y = y_0 + \frac{x_0}{R_0 - 1}[e^{(R_0 - 1)\gamma t} - 1] . \tag{12} \]

上で求めた \( x \) と \( y \) を加えた \( x + y \) は, (感染中の感染者数)＋(回復者数), つまり報道でいうところの累計感染者数を割合で表したものだ。式は煩雑になるので省略する。

図4, 図5 は, 再生産数を途中で変えたときの結果である。基本再生産数 \( R_0 \) に対して変更後つまり対策時の再生産数を「実効再生産数」と呼び, 記号も \( R_1 \) や \( R \) を使うのがふつうである。ここでは回復者数の記号との混同を避けるため, 再生産数には下付の数字を付けることにしよう。図には \( x \) (感染者数) だけでなく, \( y \) (回復者数), \( x + y \) (累計感染者数) のグラフも入れておいた。この図は数値計算を使って描いたが, 解がわかっているので式をたとえば Excel (後述) に入れるだけでも同様の図が描ける。

図 4. \( R_0 = 2.5 \) から \( R_1 = 0.5 \) (8割減) に変えたとき

図 5. \( R_0 = 2.5 \) から \( R_1 = 0.875 \) (6.5割減) に変えたとき

図4は, いわゆる8割減の効果を現すグラフだ。潜伏期を無視し, 検査で感染がわかるまでのタイムラグも無視しているので, 急に変化が現れている。本当は滑らかに変化していくと思われるが, このグラフでも傾向はわかる。 8割減が始まって再生産数が 0.5 に下がると, 数十日の時間スケールで感染者数が減っていくことがわかる。

同じ8割減のシミュレーションのグラフが専門家会議資料(4/22)の図2 に出ている (朝日新聞の4月16日の記事にもある) が, じつはあのグラフには問題がある。上の図4の赤い曲線とぴったりと重なるので同じ式を使っていると思われるが, 時間のスケールが全然違う。比較してみて, 専門家会議のグラフでは回復率に \( \gamma = 0.21 \) という値を使っていることがわかった。これは平均回復時間が 4.8 日という超高速回復率に相当する。じっさい, 専門家会議のグラフでは感染者数が10日ほどで目立って減っている。そのため, 8割減が実現すれば2,3週間で効果が現れると報道されたのだが, 本当はその数倍の時間がかかるようだ。専門家会議がなぜこのように大きな \( \gamma \) の値を使ったのかわからないが, 政治的な理由があるとしても不誠実だ。また報道機関がおかしいと気づかないのも困ったことだ。専門家会議のグラフでは感染率変更前の増え方がわずか10日で20倍にもなっていて急すぎることは, 目盛を見たら気づくはずだ。

図5は, 6.5割減で再生産数を 1 よりわずかに小さい 0.875 まで下げたときの結果だ。感染者が目立って減るまで 1 年ほどかかり, その間に累計感染者数が何倍も増えてしまうことがわかる。

最後に, 新規感染者数の計算も紹介しておこう。毎日発表される新規感染者数は, 式でいうと \( x + y \) の時間微分すなわち \( (d/dt)(x+y) \) にあたる。これは式 (8) と式 (9) を足すと得られ, つぎのように書けることがわかる。

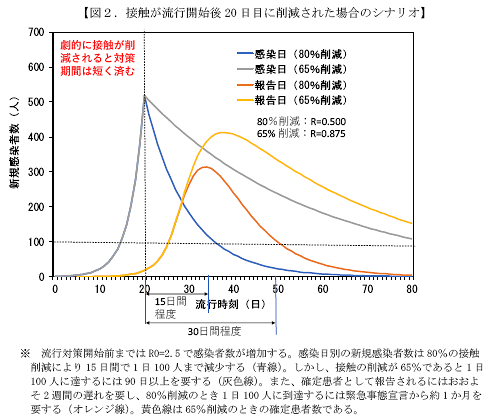
\[ \frac{d}{dt}(x + y) = R_0 \gamma x = R_0 \gamma x_0 e^{(R_0 - 1)\gamma t} . \tag{13} \]

図6 は, 図4,5 に対応する新規感染者数のグラフだ。感染率が8割減ると, 新規感染者数が本当に8割減ることがわかる。急激に変化しているのは, 潜伏期間や感染確認までの時間を無視したためで, 本当はなだらかに変化していくと思われるが, 感染率の変化が1日あたりの新規感染者数によく反映されるはずだということはわかる。じつは, 専門家会議が発表した新規感染者数のグラフ (4/22資料の図, 図6 の下に転載) はこの図のように不連続であるべきだが, なぜか感染者そのもののグラフを新規感染者のグラフとして誤って発表してしまったようだ。だいじょうぶか, 専門家会議？

ところで式 (13) から, 1日あたりの新規感染者数 \( (d/dt)(x + y) \) を回復者数を引いた感染者数 \( x \) で割ると \( R_0 \gamma \) の値が推定できることがわかる。 SIR モデルでは潜伏期間や発見までの日数を無視しているので, \( x \) は1～2週間前の値を使うのがよいだろう。

図 6. 再生産数を 2.5 から 0.5 (8割減) に変えたとき, および
2.5 から 0.875 (6.5割減) に変えたときの新規感染者数の変化

図. 感染症対策専門家会議の資料 (4/22) より。これは新規感染者数
ではなく感染者数のグラフだ。時間スケールもおかしい。
点線で描かれた水平線と垂直線も傾いているような……

Excel でシミュレーション

集団の大多数が未感染のときは, 解が指数関数を使って式 (10) － (13) のように表せるので, Excel に式を書き込むだけでグラフを描くことができる。シミュレーションというほど大げさものではないが, 再生産数を途中で変えたときのグラフを描く Excel を作ったので, 興味ある人はダウンロードして自由に使っていただきたい。なお, 計算を簡単にするため再生産数を変える日の値を初期条件としている。パラメータのいくつかを変えることができる。パラメータの記号はこのページとほぼ同じであるが, 感染者数, 回復者数として割合 \( x, y \) の代わりに人数の \( I, R \) を使っている。

Excel で使用した式を以下にまとめておく。 \( I, R \) で書くと再生産数の記号と紛らわしいので割合 \( x, y \) の式として書くことにする。再生産数を\( R_0 \)から\( R_1 \) に変える日の感染者数 \( x(t=t_1) \) を \( x_1 \) としている。この値を人数にしたら, すべて人数の式になる。

\[ \begin{align*} & x = \begin{cases} x_1 e^{(R_0 - 1)\gamma (t - t_1)} & (t \le t_1) \\ x_1 e^{(R_1 - 1)\gamma (t - t_1)} & (t > t_1) \end{cases} \\ \\ & y = \begin{cases} \frac{x_1}{R_0 - 1} e^{(R_0 - 1)\gamma (t - t_1)} & (t \le t_1) \\ \frac{x_1}{R_0 - 1} + \frac{x_1}{R_1 - 1} [e^{(R_1 - 1)\gamma (t - t_1)} - 1] & (t > t_1) \end{cases} \\ \\ & \frac{d}{dt}(x+y) = \begin{cases} R_0 \gamma x_1 e^{(R_0 - 1)\gamma (t - t_1)} & (t \le t_1) \\ R_1 \gamma x_1 e^{(R_1 - 1)\gamma (t - t_1)} & (t > t_1) \\ \end{cases} \end{align*} \]