RGB - XYZ 変換行列の求め方
ガンマ補正なしの RGB 成分を
(R, G, B),
この点の XYZ 空間での座標を
(X, Y, Z)
として,RGB から XYZ への変換行列 M
を求めよう。
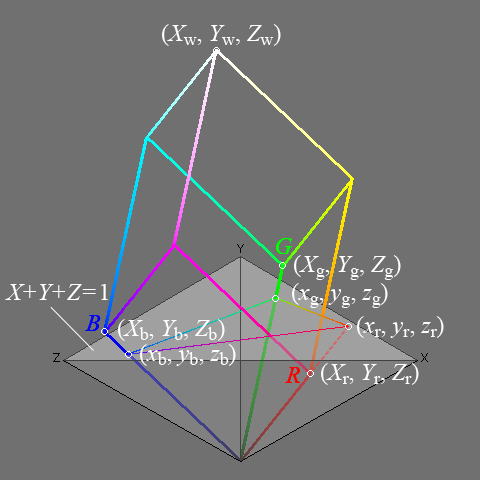
行列を決める条件として,白色点と3つの原色点の xyz 空間における座標
白色点 (Xw,
Yw,
Zw)
R点 (xr, yr,
zr)
G点 (xg, yg,
zg)
B点 (xb, yb,
zb)
が与えられているものとする (これらの値は,sRGB,Adobe RGB 等の規格で定義されている)。
ただし, (xr, yr, zr)
はR点すなわち (R, G, B) = (1, 0, 0)
の点の XYZ 空間での座標 (Xr,
Yr, Zr)
を割合で表したものである。すなわち
| xr
= Xr /
(Xr+Yr+Zr),
yr = Yr /
(Xr+Yr+Zr),
zr = Zr /
(Xr+Yr+Zr) = 1− xr− yr |
(1)
|
G点,B点についても同様とする。
もし白色点が (xw, yw) で与えられていたら,
Xw = xw / yw,
Yw = 1,
Zw = zw / yw
= (1− xw− yw) / yw
を使って換算するとよい。
さて,R点 (R, G, B) = (1, 0, 0)
を M で変換すると (Xr,
Yr,
Zr)
になることから,つぎの関係が成り立つ。
G点,B点についても同様であることから,変換行列はつぎのように表せることがわかる。
|
 |
Xr |
Xg |
Xb |
 |
|
M =
|
Yr |
Yg |
Yb |
(2)
|
|
Zr |
Zg |
Zb |
|
ところで,(1) 式より Xr は
xr に
Xr+Yr+Zr
をかけたものである。そこで
Xr+Yr+Zr = Sr,
Xg+Yg+Zg = Sg,
Xb+Yb+Zb = Sb
とおくと
Xr=Srxr,
Yr=Sryr,
Zr=Srzr,
Xg=Sgxg,
Yg=Sgyg,
Zg=Sgzg,
Xb=Sbxb,
Yb=Sbyb,
Zb=Sbzb
と表せる。
図形的には, Sr 等は ベクトル
(xr, yr, zr) 等
を ベクトル
(Xr, Yr, Zr) 等
に換算するためのスケール比のことである (図1 参照)。
こうして, 変換行列 M はつぎのように書けることがわかる。
|
 |
Srxr |
Sgxg |
Sbxb |
 |
|
M =
|
Sryr |
Sgyg |
Sbyb |
(3)
|
|
Srxr |
Sgxg |
Sbxb |
|
あるいは,2つの行列に分けて書くと
|
 |
xr |
xg |
xb |
 |
 |
Sr |
0 |
0
|
 |
M =
|
yr |
yg |
yb |
0 |
Sg |
0 |
|
zr |
zg |
zb |
0 |
0 |
Sb |
けっきょく,問題は
Sr,
Sg,
Sb
の3つを求めることに帰着する。
これらは 白色点 (R, G, B) = (1,
1, 1) が
(Xw, Yw, Zw)
に変換されることから求めることができる。すなわち,

|
Xw |

|
|
 |
1
|
 |
|
 |
xr |
xg |
xb |
 |
 |
Sr |
0 |
0 |
 |
 |
1
|
 |
|
 |
xr |
xg |
xb |
 |
 |
Sr |
 |
| Yw |
= M |
1 |
=
|
yr |
yg |
yb |
0 |
Sg |
0 |
1 |
= |
yr |
yg |
yb |
Sg |
| Zw |
|
1 |
|
zr |
zg |
zb |
0 |
0
|
Sb |
1
|
|
zr |
zg |
zb |
Sb |
これを Sr, Sg, Sb
について解くと

|
Sr |

|
|
 |
xr |
xg |
xb |
 |
−1
|
 |
Xw |
 |
|
| Sg |
= |
yr |
yg |
yb |
|
Yw |
(4)
|
| Sb |
|
zr |
zg |
zb |
|
Zw |
|
こうして Sr, Sg, Sb
が得られた。
変換行列
M は (3) 式よりただちに計算できる。
図1. XYZ 空間における色域 (sRGB) と各点の座標
補足 ― 変換行列が与えられたときの元の3原色点と白色点
(2) 式の変換行列 M がわかっているとき,簡単な計算で3原色点の座標と白色点を計算することができる。
まず,変換行列の成分を列方向に加えることで, Sr, Sg, Sb が得られる。
すなわち,
Sr = Xr+Yr+Zr,
Sg = Xg+Yg+Zg,
Sb = Xb+Yb+Zb
これより,原色点の座標はつぎのように計算できる。
xr=Xr/Sr,
yr=Yr/Sr,
zr=Zr/Sr,
xg=Xg/Sg,
yg=Yg/Sg,
zg=Zg/Sg,
xb=Xb/Sb,
yb=Yb/Sb,
zb=Zb/Sb
また,白色点は次式より得られる。

|
Xw |

|
|
 |
Xr |
Xg |
Xb |
 |
 |
1 |
 |
| Yw |
= |
Yr |
Yg |
Yb |
1 |
| Zw |
|
Zr |
Zg |
Zb |
1 |
戻る
T. Fujiwara, 2011/12, updated 2021/10