潮汐力を遠心力で説明してはいけない－ Murray & Dermott: Solar System Dynamics 修正案

英国の有名な太陽系力学の教科書 C.D. Murray & S.F. Dermott: Solar System Dynamics (1999) には, 並進慣性力を「大きさと向きが等しい遠心力」と呼ぶ間違いがある。この教科書で勉強している惑星科学の学生が多いと思われるので, 注意してほしい。剛体である惑星は並進円運動をしているだけで回転していないので, この力は遠心力ではありえない。 p132 の centrifugal force は, すべて inertial force に書き換えなければならない。
* 回転とは, 剛体が回転軸を中心に向きを変えながらまわる運動のこと。いっぽう, 並進円運動は, 向きを変えずにまわる運動のこと。高校の物理でも習うように, 回転運動と並進運動は別の運動なので, 混同してはならない。

p132 の図 (下図) のように, 並進円運動する惑星を各点の円運動に分ける説明も要注意だ。質点の運動では, 円運動はふつう回転運動として扱う。しかし, 剛体では, 並進円運動と回転運動は別の運動だ。図 4.2 の説明文には, すべての点は, 中心は異なるが同じ半径の円運動をする, と書いてある。これは, 単に惑星の運動が円に沿った並進運動であることを説明しているに過ぎない。問題は, この先だ。本文を読むとわかるように, この各点の円運動によって現れる慣性力をどこでも同じ遠心力と呼んでいる。これは, 各点の円運動を回転運動と勘違いしているためであろう。本当は, 剛体に固定された座標系が並進円運動をしているのであって, 各点が別々にそれぞれの中心のまわりを向きを変えながら回転運動しているわけではない (そもそも剛体に, 多数の回転軸をもつ回転運動などありえない)。座標系の運動は並進加速度運動なので, 惑星に現れる慣性力は遠心力ではなく, ふつうの慣性力 (並進慣性力) だ。もちろん, すべての点が同じ加速度運動をするので, 慣性力はどこでも同じになる。

このように並進円運動を各点の円運動に分けてしまうと, それを質点の運動と間違えて回転運動と勘違いするので危険だ (事実, 多くの人がそのように誤解している……)。剛体全体にはたらく力を考えるときは, 剛体を各点に分けるのではなく, 剛体の座標系にはたらく「力の場」を考えるべきだ。したがって, 惑星の運動を各点の円運動に分けるのではなく, 自転を止めた惑星の公転運動が剛体の並進加速度運動であることを強調するべきであろう。

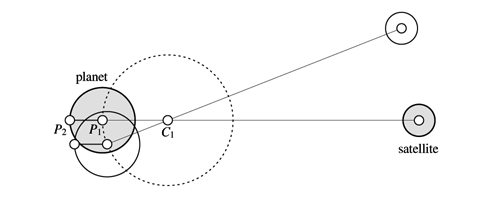Fig. 4.2. (別案) 惑星の運動が並進運動であることを示すためには, このような図で十分。円運動を回転運動と間違えないよう, 余分な円を描かないほうがよいだろう。