Color space conversion (3) XYZ-Lab conversion
XYZ to Lab conversion
In the CIE Lab space, colors are represented by three numerical values,
L*, a*, b*.
Lab is widely used in the field of color science as a homogeneous color space.
It is also used by Macintosh ColorSync as a color space for displaying various color gamuts.
Here, we will consider converting XYZ system to Lab.
First, sRGB and Adobe RGB use D65 as the reference illuminant.
On the other hand, D50 is often assumed as the standard illuminant for Lab (e.g., Adobe Photoshop uses D50 for Lab).
If the reference illuminant is different, the color of the reflected light is also different.
Before converting XYZ to Lab, therefore, we have to convert the XYZ values of sRGB or Adobe RGB colors (which assume D65 illuminant) to the colors under D50 illuminant.
This corresponds to a translation of the white point of a parallelepiped gamut of sRGB or Adobe RGB in the XYZ space.
It is common to use the Bradford transformation
for this sort of color balance adjustment (often referred to as chromatic adaptation).
This transformation is also used by Photoshop.
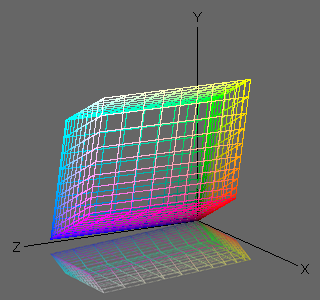
Figures 1 and 2 show the sRGB color gamut in XYZ space (under D65 illuminant), and the color gamut under D50 illuminant converted by the Bradford transform.
We can see that the white point has moved slightly to the yellow direction.
 |
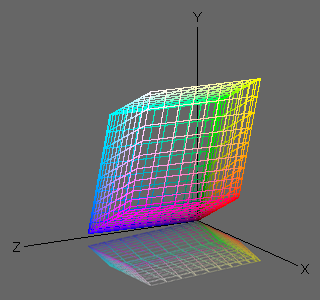 |
Fig. 1.
Color gamut of sRGB
under D65 illuminant |
Fig. 2.
Color gamut of sRGB
under D50 illuminant |
Instead of repeating conversions from RGB (D65) to XYZ (D65) and from XYZ (D65) to XYZ (D50),
it would be easier to use the conversion matrix multiplied in advance.
Table 1 gives the RGB (D65) to XYZ (D50) conversion matrix.
Table 1. RGB(D65) to XYZ(D50) conversion matrix
Color space
|
M |
M -1 |
| sRGB |
0.436041 0.385113 0.143046
0.222485 0.716905 0.060610
0.013920 0.097067 0.713913
|
3.134187 -1.617209 -0.490694
-0.978749 1.916130 0.033433
0.071964 -0.228994 1.405754
|
Display P3
P3-D65 |
0.515119 0.291978 0.157103
0.241189 0.692244 0.066567
-0.001050 0.041879 0.784071
|
2.403984 -0.989907 -0.397642
-0.842223 1.798844 0.016035
0.048206 -0.097407 1.274005
|
| Adobe RGB |
0.609741 0.205273 0.149187
0.311113 0.625675 0.063212
0.019465 0.060874 0.744560
|
1.962517 -0.610651 -0.341384
-0.978749 1.916130 0.033433
0.028715 -0.140696 1.349266
|
When the XYZ values under the D50 illuminant are obtained, the next step is to convert them to the Lab values.
This can be done by the following equations for
L*, a*, b*
using the function f (t) in equation (1).
The values of
X, Y, Z
in the parentheses of the function
f
should be divided by the coordinates
Xw, Yw, Zw
of the white point, respectively, in order to normalize the maximum values to unity.
Note that the function f (t) is switched to a straight line for small
t in order to avoid the infinite slope at the origin.
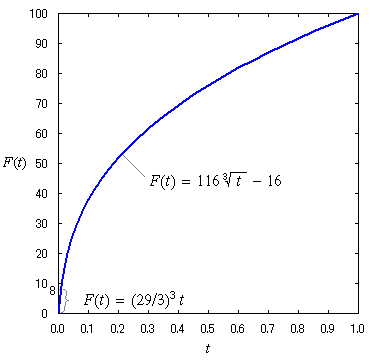
| f (t) = |
 |
t
1/3 |
if t
>
(6/29)3 =
0.008856...
|
[(29/3)3
t + 16] /116
|
otherwise |
|
(1)
|
L* = 116 f
(Y/Yw)
− 16
a* = 500 [ f
(X/Xw)
−
f (Y/Yw)]
b* = 200 [ f (Y/Yw)
−
f (Z/Zw)]
It is common to define
L*, a*, b*
using
f (t) in equation (1).
However, it seems easier to express them using
F(t)
in equation (2) below:
| F(t) = |
 |
116 t
1/3 − 16
|
if t
>
(6/29)3 =
0.008856...
|
(29/3)3
t
|
otherwise |
|
(2)
|
Using this F(t),
L*, a*, b*
can be expressed as follows:
L* = F(Y/Yw)
a* = (500/116) [F(X/Xw)
−
F(Y/Yw)]
b* = (200/116) [F(Y/Yw)
−
F(Z/Zw)]
Fig. 3. A nonlinear function for XYZ to Lab conversion
F(t)
is a function to simulates the fact that the eye response is not linear (not proportional to the lightness, known as the Weber–Fechner law), and the curve is shown in Fig. 3.
This function is used first to convert the each value of
X, Y, Z
to the brightness close to the eye response.
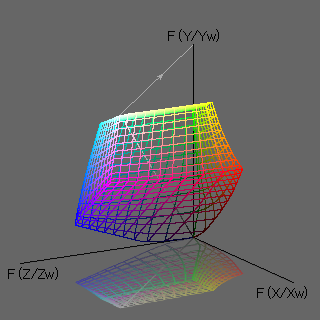
Figure 4 shows the form of the sRGB color gamut at this stage.
It can be seen that the color gamut, which is a parallelepiped in Fig. 2, is considerably deformed in Fig. 4 because the intermediate tones of
X, Y, Z
are brightened by function F(t).
The value of Y (luminosity) converted by function
F, or the height from the XZ plane in Fig. 4, is
L* (lightness).
In addition, if we set
X/Xw=Y/Yw=Z/Zw,
we get
a*=0, b*=0.
This means that the achromatic line from the origin to the white point in Fig. 4 corresponds to the
L* axis.
The values of a* and b* are obtained by multiplying the color difference from the achromatic straight line in the positive direction of the X axis and in the negative direction of the Z axis, respectively.
The Lab color space in Figure 5 is created in this way.
The axial scales of
L*,
a*, and
b*
are chosen so that the color difference may be close to the eye sensibility.
 |
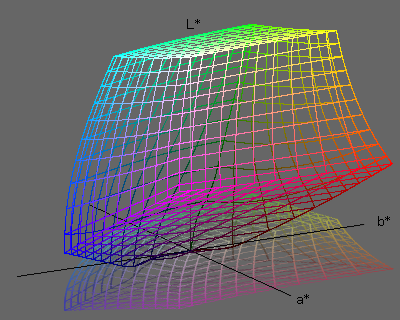 |
Fig. 4. Conversion of X, Y, and Z
using function F
|
Fig. 5. Shearing the achromatic axis as shown
by the arrow in Fig. 4 and scaling the gamut
in the X and Z directions gives the Lab space.
|
[Reference] RGB to Lab conversion viewed in the other sight direction.
[Reference] The value of L* is limited to
0—100, while values of
a* and b* vary in a wide range.
The followings are the animations of rotating color gamuts for popular color spaces:
Lab to XYZ conversion
The reverse conversion of (1) or (2) will convert the Lab values to the XYZ values.
If we write
fy
= (L*+16) / 116
fx = fy
+ (a*/500)
fz = fy
− (b*/200) ,
The XYZ values can be given by
Y = fy3Yw
(if fy > 6/29), or
Y = (3/29)3(116 fy − 16) Yw
(if fy ≤ 6/29)
X = fx3Xw
(if fx > 6/29), or
X = (3/29)3(116 fx − 16) Xw
(if fx ≤ 6/29)
Z = fz3Zw
(if fz > 6/29), or
Z = (3/29)3(116 fz − 16) Zw
(if fz ≤ 6/29).
If Lab's standard illuminant is D50, the XYZ values obtained by this inverse transformation are those under D50.
In order to convert XYZ values to RGB (sRGB or Adobe RGB) under D65 illuminant, the inverse matrix in table (2) must be used.
Furthermore, if we apply the tone correction (gamma correction), we can get
R', G', and B' values for a usual image data.
Back to content
Previous Next
T. Fujiwara, 2011/12, 2019/09