| Abstract | |
| Introduction | |
| (Additional note 1) Supplement (motion of a rigid body and inertial force) | |
| (Additional note 2) Animations (inertial forces in the earth-moon system) | |
| (Additional note 3) Textbooks in the world (foreign textbooks, Solar System Dynamics, G.H. Darwin's book, Matsuda's paper) | |
| (Additional note 4) Supplement 2: tidal force in the accelerated frame | |
| (Additional note 5) A new textbook in Japan (an earth science textbook revised in 2023) | |
| Part 1. Tidal force | |
| · Tidal force and Einstein | |
| · Tidal forces seen in the non-rotating frame | |
| · Tidal forces seen in the rotating frame | |
| · Summary of Part 1 | |
| Part 2. Tides | |
| · Misunderstanding about the phase of tides | |
| · Tidal acceleration and tidal lock | |
| (Addendum) Roche limit | |
| · Appendix of Part 2 | |
| Conclusion | |
| (Addendum) "Centrifugal force" has its roots in George H. Darwin? | |
| Links |
The expression "tidal force is the resultant force of gravity by the moon and centrifugal force due to the revolution of the earth" is often used to explain tidal force. The revolution means the earth's orbital motion around the common center of mass of the earth-moon system. In fact, high school textbooks of earth science explain tidal force as above. According to a web search, the Japan Meteorological Agency's "Tidal Mechanism" also explains tidal force in the same way (revised afterwards). Many people may have learnt this explanation in school and believed it. However, this explanation is wrong. In the first place, centrifugal force has nothing to do with tidal force. In addition, the force that should be called "translational inertial force" is mistakenly referred to by the impossible term "centrifugal force of equal magnitude and direction."
The problem of using centrifugal force to explain tidal force has been frequently pointed out by physics researchers for 30 years [e.g., Tsuneoka (1993, in Japanese), Saito (2007, in Japanese), Butikov (2017)]. In particular, Matsuda, an astrophysicist like the author, has drawn people's attention to this problem in his papers (2009, 2015) and book (2014).
The author had also noticed that the explanation using centrifugal force is incorrect, but after reading Matsuda's paper a few years ago, the depth of the problem became clear. That is, many earth science experts and astronomers are unaware of the misunderstanding in the explanation of tidal force. In fact, most of the expert commentaries and university lecture materials on the web give incorrect explanations. In this paper, the author discusses the causes of misunderstandings about tidal force and attempts to provide a correct explanation. The author hopes that this article will help correct the misleading explanations found in textbooks and on the web.
(Additional note 1) Supplement: Motion of a rigid body and inertial forces summarizes "motion of a rigid body" and "inertial forces," which are the basics for understanding the tidal force correctly. The reason why even experts make mistakes in explaining tidal force may be because they do not understand the motion of a rigid body, misunderstand the definition of centrifugal force, or do not know the term translational inertial force. In order to clear up misunderstandings about tidal force, please read this supplement first. Especially for a rigid body, please note that a distinction must be made between translational circular motion and rotation. (March 2021)
(Additional note 2) Animations showing the inertial forces appearing in the earth-moon system have been created for reference. (June 2021)
(Additional note 3)
As examples of explanations of tidal force, I have given some foreign textbooks.
In the U.S., "inertial force" is already used.
There is a problem with the textbook "Solar System Dynamics" (1999) by Murray & Dermott for university students, so I tried to correct it.
I also modified G.H. Darwin's classic masterpiece, "The tides and kindred phenomena in the solar system" (1898). (February 2022)
I modified Matsuda et.al (2015) in Amendment to Matsuda et al. (December 2022)
(Additional note 4)
Supplement 2:
Derivation of tidal force in the accelerated frame has been added. (August 2022)
(Additional note 5)
Explanation of tidal force in a new textbook of earth science in Japan has been revised. (April 2023)
The Astronomical Dictionary of the Astronomical Society of Japan explains tidal force (in Japanese) as follows: The difference between the gravitational force acting on each part of a celestial body and the gravitational force acting on the center of mass of the celestial body is called tidal force. This explanation is very clear. The object of tidal force is not limited to celestial bodies. For example, tidal force acts even on a free-falling elevator pulled by the earth's gravity. This is because the magnitude and direction of the gravitational force differ from place to place. Gravity is stronger on the side closer to the earth and weaker on the side farther from the earth. Also, since the gravity is toward the center of the earth, the gravity is slightly tilted on both sides of the elevator. Therefore, taking the difference from the gravity acting on the center of mass, we can see that the force to stretch the elevator remains in the direction of the earth and the force to squash the elevator in the direction perpendicular to the earth, as shown by the blue arrows in Fig. 1. These are the tidal forces. You may think that the tidal force that appears in such a small vehicle is weak, but it is still a force that cannot be ignored. For example, the International Space Station is free-falling toward the earth, just like an elevator. Therefore, the interior of the ISS is near zero gravity, but tidal forces remain at the periphery. Since the International Space Station is about 100 meters in size, a tidal force of a certain magnitude appears at the end. Calculations show that the tidal force is enough to move a floating object a few tens of meters in 10 minutes.
| Fig. 1. Forces acting inside a free-falling elevator. Gravity and inertia cancel each other at the center of mass, but tidal forces remain elsewhere. |
However, why do we take the difference from the gravity acting at the center of mass? For this, it is necessary to recall "inertial force." Mass has a property of maintaining its state of motion, i.e., inertia. Because of this inertia, a fictitious force appears when riding on an object in an accelerated motion. This is the inertial force. For example, when a bus starts suddenly, passengers on the bus tend to stay in place because of inertia. When this is observed inside the bus, it appears as if a backward force appears and the passengers are pulled back. In this way, the inertial force is a fictitious force that is not visible in the inertial frame, but appears only in the accelerated frame. The same applies to vertical motion. For example, when an elevator begins to descend, an upward inertial force appears and the body becomes lighter. In particular, when the elevator is in free fall under gravity, a uniform inertial force of the same magnitude as the gravity at the center and in the opposite direction appears throughout the elevator. As a result, the forces cancel each other at the center of mass, resulting in zero gravity. Thus, adding inertial force in the opposite direction of the gravity acting at the center, i.e., taking the difference from the gravity acting at the center, is a natural way to understand the forces appearing inside the free-falling elevator.
As a matter of fact, it was Einstein who noticed that gravity disappears when an object moves according to gravity. Einstein thought that gravity can be eliminated because the origin of gravity and inertial force are the same, and developed the general theory of relativity. He also called the space in which gravity disappeared (the coordinate system in free-fall) the local inertial frame. When gravity is eliminated, the space becomes a force-free space, i.e., an inertial frame. The inside of a free-falling elevator is the same inertial frame as the space far from the earth, and he thought that the coordinate system to be used as a reference frame should be this one. The reason why the word "local" is added is that only the center of mass can be gravity-free, and some gravity remains around the center due to the non-uniformity of gravity. This remaining gravity is the tidal force. By the way, the environment of the International Space Station is called a microgravity environment, not a gravity-free space, since there are still tidal forces that cannot be ignored.
Fig. 2 is an animation of free fall. Instead of the elevator, the test particles were placed in a spherical shell shape, and then released, showing how they fall under the gravitational force from the celestial body (yellow circle). The test particles are assumed to be light and do not gravitationally attract each other. When viewed from the center of the spherical shell (+), the spherical shell appears to be stretched by tidal forces (Fig. 2B). Fig. 2C shows a simulation of a galaxy encounter, although it is not free-fall. The density distribution of galaxies is assumed and stars are treated as test particles to simplify the calculation. We, astronomers, have often seen such movies and understand that tidal force is a force that deforms a celestial body due to the difference in gravity. It is the same force that acts on a free-falling elevator. As shown in Figure 2, tidal force appears simply when an object with a size is subjected to gravity. It has nothing to do with rotation. If this is explained in terms of centrifugal force, we think "what?"
 |
 |
 |
| Fig. 2. Animation of a free-falling spherical shell. Each point on the spherical shell is just falling toward the yellow circle. | Fig. 2B. Animation of a free-falling spherical shell. Viewed from the center of the spherical shell. | Fig. 2C. Animation of the tidal deformation of galaxies associated with a galactic encounter. |
In Fig. 3, the free-falling elevator is replaced by the earth "free-falling" toward the moon.
When viewed on the earth, a uniform inertial force appears on the entire earth due to the acceleration toward the moon.
The magnitude of the inertial force is equal to the moon's gravity at the center of the earth,
and its direction is opposite to that of the gravity.
Turning this figure 90° clockwise, it is almost the same as Fig. 1.
* In this explanation, we will consider the tidal force only due to the moon, for simplicity.
In reality, the earth is also subject to the tidal force of the sun.
Its magnitude is about 0.46 times as large as that of the moon.
| Fig. 3. Tidal force (blue) is the resultant force of the gravity (light blue) acting on each point of the earth and the inertial force (pink) acting uniformly on the whole earth. At the earth center, the gravity and the inertial force just cancel each other. |
The difference from the elevator is that the earth and the moon are moving sideways so that they do not collide with each other, in so-called orbital motion. Based on the ratio of their masses, the common center of mass of the earth-moon system is located inside the earth, and the earth and the moon revolve around this common center. (The fact that the common center of mass is inside the earth is not essential to the discussion to come.) Fig. 4 is a redrawn figure including the earth's orbital motion. For simplicity, a circular orbit is assumed. As in Fig. 3, the earth's rotation is stopped (or rather, no extra motion of the earth is considered). The direction of the earth's motion gradually turns toward the moon due to the gravity of the moon, of course. Thus, although there is a difference that the earth is falling down while dodging to the side compared to Fig. 3, there is no change in the fact that a uniform inertial force appears on the earth due to the earth's acceleration toward the moon. This uniform inertial force is sometimes called "translational inertial force" in the sense that it is caused by translational accelerated motion. We will use this terminology here as well.
| Fig. 4. Due to the translational acceleration of the earth by being pulled by the moon, i.e., translational circular motion around the common center of mass, an inertial force (not centrifugal force!) that acts uniformly on the entire earth appears when viewed from the earth. |
Some people (and most textbooks) call this uniform inertial force or translational inertial force "centrifugal force," but this is incorrect. This is because the earth is not rotating with respect to the inertial frame of reference. Therefore, this inertial force cannot be centrifugal force. The earth is just in accelerated translational motion along the circle without changing its orientation. The force appearing on the earth in accelerated translational motion should be translational inertial force, just like in a free-falling elevator.
It is often explained that the reason why the magnitude of inertial force in Fig. 4 is the same everywhere is because each point of the earth is moving in a circle of the same radius. However, the explanation that divides the earth into many points in circular motion is misleading. In fact, many people misunderstand the circular motion of each point as rotational motion and mistake translational inertial force for centrifugal force. Even the textbook Solar System Dynamics (2000) for university students calls this force "centrifugal force of equal magnitude and direction." The reason why the magnitude and direction of inertial forces are equal everywhere is simply because the earth is in translational accelerated motion as a rigid body. In the accelerated translational motion of a rigid body, all points have the same motion with respect to the inertial frame, so it is natural that the inertial forces are equal everywhere. Again, this inertial force is due to the translational motion, not the rotational motion, so we should not call it centrifugal force. (See Supplement: Motion of a rigid body and inertial forces for the difference between translational circular motion and rotational motion.)| Fig. 5. Coordinates for the earth-moon system with the center of the earth as the origin. |
Here, let us use a few equations. Since we are using only the knowledge of physics of a first-year college student, it should be easy to understand for those who have a science background. First, we consider the forces only in the direction of the moon. As shown in Fig. 5, the center of the earth is the origin, the position of a point on the earth is \( x \) and the distance to the moon is \( a \). If the mass of the moon is \( m \) and the gravitational constant is \( G \), a point on the earth is subject to the moon's gravity per unit mass, \( f \), which is inversely proportional to the square of the distance to the moon, \( a-x \). If \( x \) is sufficiently small compared to \( a \), the gravity \( f \) can be approximated by the following equation:
The first term on the right-hand side represents the gravity of the moon at the center of the earth, or the average gravity that the entire earth receives from the moon. The second term is the difference between the gravity of the moon at a point on the earth and at the center of the earth, i.e., the tidal force. The force \( f \) is, of course, seen from the inertial frame of reference. If we see this force on the earth accelerated by the moon, the inertial force that is just opposite to the moon's gravity at the earth center appears. Thus, the force seen on the earth, \( f' \), can be written as the resultant force of \( f \) and \( -Gm/{a^2} \). Consequently, only the tidal force remains:
This is the well-known formula of tidal force in the direction of the moon. Thus, the tidal force can be expressed as the resultant force of the moon's gravity and the uniform inertial force, or as the difference between the moon's gravity at a point on the earth and the moon's gravity at the earth center. On the side closer to the moon, the moon's gravity exceeds the inertial force, leaving the tidal force in the direction of the moon. On the far side from the moon, the inertial force exceeds the moon's gravity, leaving the tidal force in the direction opposite to the moon. As can be seen from the above discussion, tidal force appears when the earth is simply in accelerated motion under gravity. Revolution of the earth is not necessary at all. Tidal force appears even if the earth moves straight toward the moon or even if it stops momentarily.
Here we used the potential, which can represent the force field in a concise form. If we use the force directly, we have to consider a vector equation or write separate equations for each component of the force. From the definition of potential, the force can be obtained by differentiating the potential and changing the sign. For example, differentiating the potential equation by \( x \) and changing the sign yields the \( x \) component of the force.
The second term in Eq. (3) is the gravitational potential due to the moon. Let this term be \( V_{\rm{m}} \), assuming that \( x \), \( y \), and \( z \) are sufficiently small compared to \( a \), and expanding it to a second order term, we find that it can be approximated by the following equation:
The first term is a constant and can be ignored. The second term represents the uniform force that the entire earth receives from the moon, or the gravity acting at the center of the earth. The third term represents the tidal force, or the deviation of gravity at each point from the gravity acting at the center of the earth. (This equation can also be obtained using the Legendre polynomial.)
Now let us move to the coordinate system of the earth in acceleration toward the moon. In the accelerated frame, translational inertial force appears as in the interior of an elevator. Since this inertial force has the same magnitude and opposite direction as the gravity given by the second term in Eq. (4), the second term vanishes in the accelerated frame. Consequently, viewed from the earth, only the earth's gravity and the tidal force are visible. Thus, the potential representing the force in the accelerated frame can be approximated by the following equation, excluding the constant term (see Supplement 2: Tidal force in the accelerated frame for derivation of the potential using the equations of motion).
By differentiating the second term of this potential, we can obtain the magnitude of the tidal force per unit mass, or the tidal acceleration. If we write the tidal acceleration as \( \boldsymbol{f'} \), the tidal acceleration is \( f'_{x} = 2Gmx/{a^3} \) in the direction of the moon and \( f'_{y} = -Gmy/{a^3} \) in the direction perpendicular to the moon. The tidal accelerations calculated using these equations are the values shown in Fig. 6. Compared with the gravitational acceleration of 9.8 m/s2 on the ground surface, the tidal acceleration in the direction of the moon is about one ten millionth of that, while the tidal acceleration perpendicular to the moon is another half.
| Fig. 6. Forces per unit mass acting on each point of the earth. Since the ratio of the distances to the moon from the far side, the center, and the near side of the earth is approximately 61:60:59, the ratio of the magnitude of gravity (light blue) is approximately 29:30:31. On the other hand, the force that opposes the gravity at the center is the translational inertial force (pink). You can see that the tidal force (dark blue) is much smaller than the gravity and the translational inertial force. |
Next, we consider the displacement of the equipotential surface of the earth due to the tidal force. Let \( R \) be the radius of the earth and \( \zeta \) be the rise of the equipotential surface in the direction of the moon. The sum of the gravitational potential and the tidal potential on the raised equipotential surface is obtained by putting \( x = R+\zeta \) in Eq. (5), that is
The change in the tidal potential (the last term) due to the rise of the equipotential surface is neglected because it is sufficiently small. Since Eq. (6) is equal to the potential in the absence of tidal force, \( -GM/R \), the rise of the equipotential surface in the direction of the moon is obtained as follows:
Similarly, the following equation is obtained in the direction perpendicular to the moon:
The numerical values are +0.36 m in the direction of the moon and −0.18 m in the direction perpendicular to the moon. A difference of ±27 cm from the mean level, or a tidal range of 54 cm. This is the magnitude of the tidal force due to the moon.
Fig. 7 shows the direction and magnitude of tidal forces at various points on the earth's surface. A similar figure appears on the English page of Wikipedia, but please note that the figure is inaccurate (cf. a revised version by the author). For reference, if you connect the tips of the arrows in Fig. 7 with a smooth line, you will get an ellipse. If the tips of the arrows are not on the exact ellipse, the figure can be considered crudely drawn.
| Fig. 7. Tidal forces at various points on the earth. |
The following figure shows the contours of the tidal potential around the earth (the second term of Eq. (5) ) superimposed on Fig. 7.
| Fig. 7'. Tidal potential around the earth. |
As we have seen above, rotational motion is not necessary to explain tidal force. However, in the translational frame shown in Figure 4, the coordinates of the moon and the earth change with time, and the direction of the translational inertial force also changes (see this animation). Therefore, Eqs. (3), (4), and (5) are valid only for an instant. To avoid this, it is better to ride on a rotating frame that rotates with the revolution. Now we assume that the earth is at rest with respect to the rotating frame. In this case, the extra fictitious force such as the Coriolis force do not appear, and there is no time variation of the force acting on each point of the earth, which makes it easier to understand the force field.
By the way, centrifugal force, which is a fictitious force, always appears in a rotating frame. Centrifugal force is an outward force around the axis of rotation, and its magnitude is proportional to the distance from the axis. Looking at the earth from the north, the centrifugal force around the common center of mass is as shown in Fig. 8. Textbooks say that "tidal force is the resultant force of gravity by the moon and centrifugal force around the common center of mass." However, comparing Fig. 8 with Fig. 3, it is clear that the resultant force of the gravity of the moon and this centrifugal force does not result in tidal force. In fact, for example, the magnitude of the resultant force in the direction of the moon is 46.4×10−6 m/s2, which is 42 times the tidal force in Fig. 6 (assuming that the mass ratio of the earth to the moon is 81). In other words, if the tidal force is calculated honestly as explained in the textbooks, it will not be the correct value. The counterpart of the resultant force of gravity by the moon must be the inertial force represented by the pink arrow in Fig. 3, not the centrifugal force. Then, where does this inertial force come from when viewed on the rotating frame?
| Fig. 8. Centrifugal force around the common center of mass, appearing in the rotating frame. |
Let us use the equation again. It may be natural to use a coordinate system whose origin is the common center of mass. However, since what we want to know is the force whose origin is the center of the earth, we will use the same coordinate system as in Fig. 5. In this case, both the earth and the moon are at rest with respect to the coordinate system since the system rotates together with the earth-moon system. Now, in a rotating frame, centrifugal force always appears. The Centrifugal force acts radially in a direction perpendicular to the axis of rotation, and its magnitude is proportional to the distance from the axis of rotation. This force can be expressed as a potential proportional to the square of the distance from the axis of rotation. Thus, the potential in a rotating frame is the sum of the gravitational potential of the earth (mass \( M \)), the gravitational potential of the moon (mass \( m \)), and the centrifugal potential. That is,
The second term is the gravitational potential due to the moon, and the third term is the centrifugal potential. We have already mentioned that the gravity potential due to the moon can be approximated as in Eq. (4). On the other hand, since the centrifugal force is proportional to the distance from the axis of rotation, the centrifugal potential is proportional to the square of the distance. Let \( V_{\rm{c}} \) be the centrifugal potential,
where,
Here \( {\Omega} \) is the angular velocity. Expanding Eq. (10) and rewriting it using Eqs. (11) and (12), we find that the centrifugal potential can be written as follows:
In the second line of the above equation, the first term represents the uniform inertial force, or translational inertia, and the second term represents the centrifugal force around the earth center. This means that the centrifugal force around the common center of mass can be decomposed into translational inertial force and earth-centered centrifugal force. The third term is a constant and can be ignored. By differentiating this potential and changing the sign, we can obtain the force field illustrated in Fig. 9.
| Fig. 9. The centrifugal force around the common center of mass (red) can be decomposed into translational inertial force (pink) and earth-centered centrifugal force (yellow). |
After all, the sum of \(V_{\rm{m}}\) in Eq. (4), i.e. the gravity of the moon, and \(V_{\rm{c}}\) in Eq. (13), i.e. the centrifugal force around the common center of mass, becomes the following simple equation, because the second term of Eq. (4) and the first term of Eq. (13) cancel each other. That is,
The first term on the right side is the tidal force, and the second term is the centrifugal force around the earth center. In this way, in a rotating frame, centrifugal force always appears in addition to tidal force. Moreover, the magnitude of the centrifugal force is much larger than that of the tidal force (\((M+m)/(2m)\) times, or about 41 times, the tidal force in the direction to the moon). Thus, when a rotating frame is used to explain the tidal force, the large earth-centered centrifugal force appears and makes the tidal force difficult to see. In addition, it is necessary to explain why the centrifugal force appears. It would be wiser to explain the tidal force without depending on the rotating frame.
For reference, this centrifugal force is due to rotational motion with a period of 27.3 days. Since this centrifugal force is centered on the earth, it only works to expand the earth in all directions along its orbital plane and does not contribute to the tides. In reality, the earth rotates with a shorter period of 24 hours and 50 minutes with respect to the rotating frame (or 23 hours and 56 minutes with respect to the inertial frame), so the earth is considerably expanded in the equatorial direction.
It was found that even if the earth rotates along with its orbit, a translational inertial force appears. When this translational inertial force and the gravity by the moon are added together, the tidal force comes out properly. Just because the translational inertial force comes out as a component of the centrifugal force, it should not be called by a confusing name such as "parallel component of centrifugal force." There is a proper term "translational inertial force", so it should be used.
The fact that translational inertial forces appear when centrifugal forces are viewed from a position other than the axis of rotation is well illustrated by representing the force field with arrows. Fig. 10 shows the centrifugal force field around the common center of mass viewed from the z-axis. The common center of gravity is at the center of the figure. When the centrifugal force field is viewed from the axis, it looks radial like this.
|
|
|
Fig. 10. Centrifugal force field appearing around the common center of mass in a rotating frame.
G is the common center of mass. * Mouseover to show the earth. |
The centrifugal force field in Fig. 10 can be resolved into two force fields: translational inertial force field (Fig. 11) and earth-centered centrifugal force field (Fig. 12). These figures are basically the same as Fig. 9. The only difference is that the figure of the earth is omitted and the forces are drawn in separate figures for each component. When considering the force seen from the earth center, it is easier to understand by decomposing the force into components like this. Fig. 11 and Fig. 12 correspond to the first and second terms in Eq. (13), respectively. It would be easy to imagine that the superposition of the forces in Fig. 11 and Fig. 12 would result in the centrifugal force in Fig. 10 (see Fig. 10'). It will also be clear that the force shown in Fig. 11 is not the "centrifugal force." For reference, it is written in Landau-Lifshitz's mechanics textbook that translational motion appears in addition to rotational motion when the axis of rotation is moved to a position other than the common center of mass. The force associated with this translational motion is the translational inertial force.
|
|
|
| Fig. 11. Translational inertial force component acting on the whole earth when the centrifugal force around the common center of mass is decomposed. * Mouseover to show the earth. |
Fig. 12. Centrifugal force component around the earth center when the centrifugal force around the common center of mass is decomposed. O is the earth center. * Mouseover to show the earth. |
A simple and clear explanation of tidal force would be "the difference between the gravity of the moon at each point of the earth and the gravity of the moon acting at the center of the earth." Instead of taking the difference from the force at the earth center, we can add the force in the opposite direction and explain tidal force as "the resultant force of the moon's gravity at each point of the earth and the translational inertial force acting on the entire earth due to the earth's accelerated motion." Thus, there is no need to bring up centrifugal force in the explanation of tidal force.
Textbooks and many commentaries incorrectly refer to this translational inertial force as "centrifugal force of equal magnitude and direction." In the first place, centrifugal force is a radial force whose magnitude is proportional to the distance from the axis of rotation. Thus, there is no such thing as centrifugal force of equal magnitude and direction. This misuse of "centrifugal force" is probably because they forget that the earth is a rigid body and confuse translational circular motion with rotational motion. "Centrifugal force" in textbooks should be changed to "inertial force" as soon as possible.
Furthermore, using the term "centrifugal force" implies that one is in a rotating reference frame. In other words, if one inadvertently uses the term "centrifugal force" with the intention of using translational inertial force, the term would have been used to mean the original centrifugal force that appears in a rotating frame against one's will. Thus, misuse of "centrifugal force" inevitably leads to confusion. The term "centrifugal force" should, of course, be used only in its original meaning (i.e., a radial force that appears in a rotating frame).
Next, let us consider tides as a phenomenon. Earth's tides are mainly caused by the tidal force of the moon. (The tidal force of the sun is also about 0.46 times that of the moon, but we will not consider it here.) Since the earth rotates with a short period of 24 hours and 50 minutes relative to the rotating frame on its orbit, high tide occurs every 12 hours and 25 minutes at a fixed point on the earth. In the textbooks, a figure of the earth with two bulges of seawater, one near the moon and the other on the opposite side, appears as an explanation. Such a figure is based on the assumption that the deformation of the sea level is fast enough to keep up with the change in tidal force and reach an equilibrium state. In reality, however, sea level deformation is slow, and the shape of the sea surface does not change as shown in the textbooks. For example, on the Pacific coast of western Japan, high tide is about 6 hours later than the culmination of the moon, and low tide occurs when the moon is in the south. This is because the tidal pattern of the oceans is complicated and the timing of high and low tides happen to be reversed on the Pacific coast of western Japan. There are many people on the Internet who take this point alone and claim that the textbook's explanation is wrong. The logic is as follows. Tides are a matter of forced oscillations due to external tidal forces. The speed of the tidal phase relative to the earth is 400 m/s, whereas the speed of long waves traveling in the ocean is only about 200 m/s. When the external force changes too fast to respond, the phase of the oscillation should lag behind the external force by nearly 180° according to the theory of forced oscillations. Therefore, the figure in the textbooks is wrong, and the sea level should always be bulging in the direction 90° away from the moon. The tides on the Pacific coast of western Japan prove it, and so on.
This description oversimplifies the problem. This is because ocean oscillations must be considered as a problem of waves, not as a problem of a point mass. For waves, local deformation and resonance following changes in tidal forces are possible because there can be harmonics with short wavelengths and short periods. In fact, tidal phases vary from place to place and are not 180° out of phase everywhere. (However, the analogy between ocean tides and forced oscillations with resistance seems to hold to some extent. As described below, when averaged over the entire globe, the phase of ocean tides and that of tidal forces are significantly out of phase.)
The actual ocean has a complex shape, divided by continents. The depth of the oceans also varies from place to place. In addition, because of the earth's rotation, seawater is subject to the Coriolis force when it moves. This further complicates the motion of seawater. When the Coriolis force acts, there are two modes of waves: inertial waves, which are similar to ordinary long waves, and Kelvin waves, which were theoretically discovered by Lord Kelvin in the 19th century. Kelvin waves are such that their amplitude reaches a maximum at the coast, and in the northern hemisphere they propagate with the coast to the right. In the North Atlantic Ocean, for example, Kelvin waves resonating with tidal forces rotate counterclockwise. Resonant Kelvin waves are also rotating in shallow bays around the world. On the other hand, the Pacific Ocean is so wide that the waves seem to be divided into several basins.
At the end of the 19th century, the wave pattern of ocean tides was analyzed by dividing it into several components (called tidal constituents) with specific periods. For example, the tidal constituent due to the moon with a period of 12 hours and 25 minutes is called M2, the tidal constituent due to the sun with a period of exactly 12 hours is called S2, and the tidal constituent due to the inclination of the earth's rotation axis with a period of 23 hours and 56 minutes is called K1. The O1 tidal constituent (with period of 25 h 49 min), whose frequency is equal to the difference between the frequencies of M2 and K1, is also relatively large in amplitude. In the 1990s, ocean tide models based on satellite tide level observations and numerical calculations were developed, making it possible to reproduce tides fairly accurately by synthesizing tidal constituents. Figures 13 - 18 show the tidal pattern (M2 constituent) by the ocean tide model. Although it is difficult to see in detail, there are many places along the coast where the tidal range is large due to resonance. In this way, the oceans respond to changes in tidal forces associated with the earth's rotation by creating complex patterns. The ocean tide models NAO.99b / NAO.99Jb by the National Astronomical Observatory of Japan (NAOJ Mizusawa) were used to create these figures.
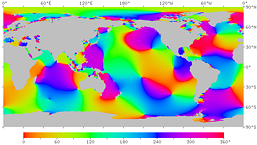 |
 |
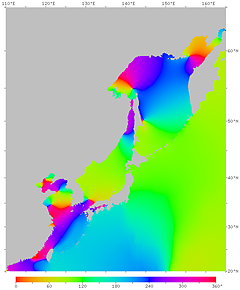
| Fig.14. Phase of the M2 tidal constituent due to the moon. The high tide time (in GMT) at each point is expressed in phase angle. The right figure has contour lines. | |
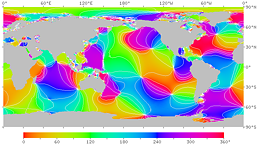
 |
 |
| Fig.14'. Phase lag of the M2 constituent. The time from the moon's meridian transit to high tide at each point is expressed as a phase angle. The angle of 360° corresponds to 12 hours and 25 minutes. The right figure has contour lines. | |
 |
 |
| Fig.15. Animation of the M2 tidal constituent due to the moon. The angle in white is the time (GMT) expressed in phase angle. Left: GIF animation, Right: manual animation. | |
 |
 |
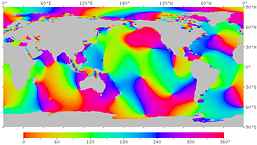
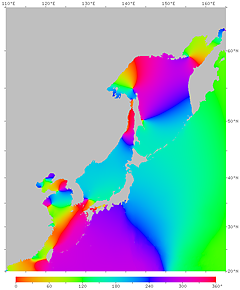
| Fig.17. Phase of the M2 tidal constituent due to the moon. The high tide time (in GMT) at each point is expressed in phase angle. If the tidal phase were in phase with the moon, the high tide time at 135°E would be −270° (about −9 h), or +90°. However, it is actually about 260° on the Pacific coast around there. | |
 |
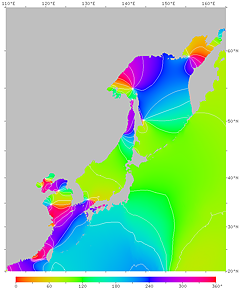 |
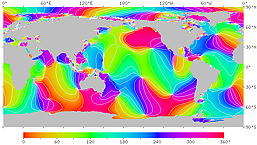
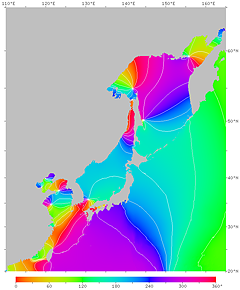
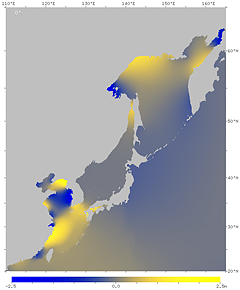
| Figure 17'. Phase lag of the M2 constituent. The time from the moon's meridian transit to high tide at each point is expressed as a phase angle. The angle 360° corresponds to 12 hours and 25 minutes. The right figure has contour lines. It can be seen that there is a delay of about 4 hours along the Pacific coast of northern Japan, about 6 hours along the Pacific coast of western Japan, and about 11 hours on the central Seto Inland Sea. | |
 |
 |
| Fig.18. Animation of the M2 tidal constituent due to the moon. The angle in white is the time (GMT) expressed in phase angle. Left: GIF animation, Right: manual animation. | |
Fig. 19 is a conceptual diagram of the tidal bulge due to the moon. The real ocean tidal pattern, as we have seen above, is bumpy due to resonances that occur in various parts of the ocean. The phase of the tides also varies from place to place. In order to average such a complex tidal pattern, if the tidal constituent M2 of the ocean tide model are decomposed into spherical harmonic components, the amplitude of the principal component (half of the tide difference) is 9.6 cm, according to the author's calculation. (Wikipedia's "Tidal acceleration" states that the amplitude is 3.23 cm, which seems to be a misrepresentation of the coefficient defined to be the amplitude when multiplied by three.) In addition, the direction of the principal component of M2 is shifted toward the earth's rotation by about 65° from the direction of the moon. This means that, on the earth, high tide arrives when the moon moves 65° (4.5 hours later) on average after the meridian transit. This is because the tidal deformation of the ocean is dragged in the direction of the earth's rotation by friction with the seafloor. The contribution to friction is large in the coastal areas where the resonance causes faster currents.
On the other hand, the solid earth is also deformed by tidal forces. Due to the hardness of the earth, the deformation is only about 0.6 times (amplitude of about 15 cm) of the equilibrium shape (amplitude of 27 cm) caused by tidal forces, but it is still large. The direction of tidal deformation of the solid earth also deviates slightly from the direction of the moon due to the internal friction of the earth. However, the deviation is estimated to be very small (about 0.1° in angle). In addition, the solid earth also undergoes secondary deformation due to load changes caused by ocean tides. The magnitude of the vertical variation seems to be about 1 cm. The net tidal deformation of the solid earth combined with that of the ocean results in an angular shift of about 3° relative to the direction of the moon, as shown in Fig. 19.
In illustrations of tides often seen in textbooks, the solid earth remains unchanged and only the oceans are deformed. In reality, however, the amplitude of the solid earth is about 15 cm, and the amplitude of the ocean is about 10 cm, so the deformation of the solid earth is larger. Furthermore, the direction of deformation of ocean tides deviates greatly from the direction of the moon. However, because the density of seawater is smaller than that of the solid earth and the average amplitude of ocean tide is also small, the deviation of the net tidal deformation of the earth as a whole is only 3 °.
| Fig. 19. The direction of tidal deformation, which is a composite of ocean tide (blue) and solid earth tide (brown), is slightly deviated from the direction of the moon due to the earth's rotation. | Fig. 19'. According to the observations, the angle of deviation of the ocean tide (blue) is about 65°. On the other hand, the deviation of the solid earth tide (brown) is about 0.1°. When these are composed, the result is as shown in the left figure. |
The tidal effects of the moon are not limited to the deformation of the earth. The moon itself, which deforms the earth, is also greatly affected by the earth, i.e. the earth deformed as shown in Fig. 19 pulls the moon in the direction of travel. As a result, the moon moves away from the earth and at the same time the earth's rotation slows down. This phenomenon is known as tidal acceleration. Using the conserved quantity "angular momentum", we can say that the angular momentum of the earth's rotation is transferred to the orbital angular momentum of the moon. The distance to the moon can be measured by reflecting a laser beam with the reflector that Apollo left on the moon's surface. The rotation period of the earth can be determined by star observations. According to these observations, the moon is moving away from the earth at a speed of 3.8 m per century. The length of the earth's day increases by about 2 milliseconds per century, which adds up to a time lag of about 30 seconds per (century)2 (proportional to the square of time).
Fig. 20 shows the angular momentum of the earth and the moon as a function of the moon's orbital radius, respectively. According to the theory of tidal acceleration, the orbital radius of the satellite is proportional to the 13th root of the square of time. The times indicated by the arrows on the graph are calculated assuming that the parameters of tidal acceleration (the friction of the sea water and the deformability of the earth) are always constant. According to these calculations, about 50 billion years from now the earth's rotation will have a period of 47 days, synchronized with the orbital period of the moon. By the way, compared to the parameters averaged over the last 4.5 billion years used in this figure, the earth seems to have been much more prone to tidal deformation in the last few hundred million years. In fact, the measured tidal acceleration is about three times faster than the average for the past. It is thought that changes in the shape of the oceans due to continental drift and the lengthening of the rotation period may be causing the oceans to resonate more easily with tidal forces, leading to greater friction. At this rate, the synchronization of the earth's rotation and the moon's orbital motion will probably occur much earlier. Furthermore, the slowing of the earth's rotation by the sun, which is ignored in the above calculation, will also come into play. Even so, it may be difficult to achieve synchronization during the lifetime of the sun.
| Fig. 20. Changes in the orbital angular momentum of the moon and the rotational angular momentum of the earth due to tidal acceleration. Days near the curves are the earth's rotation period and the moon's orbital period. The arrows indicate the estimated time from the formation of the moon. |
As mentioned above, the earth is affected by the moon, which has only 1/81 of the mass of the earth. On the other hand, the tidal force that the moon receives from the earth is much larger, and its influence is enormous. For example, the tidal force that the moon receives at the current orbital radius is 13 m in the direction of the earth when converted to the height on the moon surface. Moreover, the newly formed moon is thought to have been at a distance only several times larger than the earth's radius. Since the tidal force is inversely proportional to the cube of the distance, the tidal force that the moon received at that time was about 1000 times stronger than it is now, corresponding to a height of more than 10 km. The moon, which was rotating, is greatly deformed by the tidal force, and the deformed moon loses its rotational angular momentum rapidly as it tries to pull the earth. As a result, the moon stops rotating in a short time. The time is only about 1000 years, even if the moon were at a distance of 10 times the earth's radius. In this way, the tidally deformed moon is locked to the rotating frame with the same side facing the earth (Fig. 21). This process is called tidal locking. This is the reason why the moon always faces the same side toward the earth.
Tidal locking has been realized for the major satellites of the solar system with their unique names. This is because the large mass of the parent planet causes severe tidal deformation, leading to tidal locking of the satellite in a short time. Exceptions are Saturn's satellite Hyperion (which is rotating chaotically in resonance with the orbital motion of Titan) and such satellites orbiting away from the parent planet as Saturn's satellite Phoebe or Neptune's satellite Nereid (they are still rotating). In the case of Pluto, a dwarf planet with a relatively large satellite, not only the satellite Charon but also Pluto itself is already in a tidally locked state and mutual locking has been achieved.
| Fig. 21. Most major satellites in the solar system are tidally locked. |
Next, let us consider the shape of a tidally locked satellite. Since a locked satellite is at rest with respect to a rotating frame, it is appropriate to consider it in a rotating frame. Since centrifugal forces appear in a rotating frame, the satellite is subjected to both tidal and centrifugal forces. Assuming that the satellite is the earth's moon, the expression for the potential energy with the origin at the center of the moon can be obtained by simply switching the positions of the earth and the moon in Eq. (14). Now, if the potential due to the earth's gravity is \( V_{\rm{e}} \), and the centrifugal potential due to the orbital motion is \( V_{\rm{c}} \), then
Assuming that the mass of the moon \( m \) is much smaller than the mass of the earth \( M \), and neglecting \( m \) in \( M+m \), the above equation becomes
The first term is the tidal force due to the earth and the second term is the centrifugal force around the moon center. As can be seen from the equation, the tidal force and the centrifugal force are of the same order of magnitude for a satellite with a small mass.
| Fig. 22. Deformation of a tidally locked satellite due to tidal force. | Fig. 23. Deformation of a tidally locked satellite due to centrifugal force. | Fig. 24. Deformation of a tidally locked satellite due to both tidal force and centrifugal force. |
Differentiating this equation to obtain the magnitudes of the tidal and centrifugal forces on the moon surface, the magnitudes in the x, y, and z directions are +2 : −1 : −1 for the tidal force and 1 : 1 : 0 for the centrifugal force in units of \( (GMr)/{a^3} \), where \( r \) is the radius of the moon. The ratio of the magnitude of deformation due to these forces is +2 : −1 : −1 for tidal deformation and +1/3 : +1/3 : −2/3 for centrifugal deformation (normalized so that there is no change in the volume). Combining these deformations, the ratio of the magnitude of deformation in the x, y, and z directions is +7/3 : −2/3 : −5/3 (see Figures 22 to 24). If the satellite is soft enough, it should deform at this ratio. In reality, satellites do not seem to follow the theory because they solidify at some stage and then slowly deform. (Note. In the above discussion, I suggested that the object deforms simply according to the shape of the potential. This picture is correct only when the mass is concentrated at the center of the object. In reality, the deformation is larger than the simple calculation because the potential also changes with the deformation of the object.)
In schools, we are taught that the moon always faces the same side toward the earth because its rotation period and orbital period coincide with each other. However, this is just a rewording of the same phenomenon, not an explanation of the cause. The real cause is that the moon is "stuck" in a force field distorted by the tidal force due to the earth. In school education, in connection with the topic of tides, it may be worth mentioning that the moon is also subjected to tidal forces by the earth. At least, teachers should know about tidal locking.
(Addendum: Roche limit 2023/03)
In relation to the tidal acceleration, let me explain the Roche limit.
When the orbital period of a satellite is longer than the rotation period of the planet, as in the case of the moon, the satellite is accelerated and moves away from the planet.
However, when a satellite is close to the planet and its orbital period is shorter than the rotation period of the planet, as in the case of Phobos on Mars, the satellite is decelerated and moves closer and closer to the planet.
And when the satellite gets too close to the planet, the tidal force by the planet will exceed the self-gravity of the satellite, causing rocks on the near side and far side of the satellite to rise up like Laputa and destroying the satellite.
In such a case, the orbital radius at which the satellite can remain undestroyed is called the Roche limit.
Unfortunately, there are many cases on the internet where the Roche limit is incorrectly calculated, so I would like to explain it here.
In situations where a satellite is so close to a planet that tidal breakdown becomes a problem, the satellite should have already been tidally locked. Therefore, the forces acting on the satellite must be considered in the rotating frame. That is, both tidal and centrifugal forces act on the satellite. If the mass of the satellite \( m \) is much smaller than the mass of the planet \( M \), the tidal and centrifugal potentials are given by Eq. (16). Differentiating this equation by \( x \), we can obtain the tidal force + centrifugal force (per unit mass) in the \( x \) direction. If the radius of the satellite is \( r \), the tidal force + centrifugal force at the surface of the satellite is given by
On the other hand, the self-gravity of the satellite on the surface is
The orbital radius \( a \) of the satellite where these two forces are balanced is the Roche limit. That is
Now we assume that the interiors of the planet and the satellite are uniform, and let their densities be \({\rho _{\text{M}}}\) and \({\rho _{\text{m}}}\), respectively. If the radius of the planet is \( R \), we can write \(M = (4\pi /3){\rho _{\text{M}}}{R^3}\) and \(m = (4\pi /3){\rho _{\text{m}}}{r^3}\). Thus Eq. (19) can be rewritten as follows:
This is the Roche limit when the satellite is assumed to remain spherical and not deform, so it is sometimes called the rigid limit. You may often see an equation where the coefficient in the parentheses is 2 instead of 3 (e.g. Wikipedia). That is because they have forgotten that the satellite is in tidal lock and missed to add the centrifugal force.
On the other hand, if the satellite is assumed to deform freely like a liquid, the Roche limit is larger than the above equation because the satellite deforms according to the potential, becomes elongated and breaks at an early stage. According to the calculation, the Roche limit in this case is as follows:
This Roche limit is sometimes called the fluid limit. The value in Eq. (21) are based on the assumption that the satellite density is uniform. However, it is natural that the satellite density is higher closer to the center. In such a case, the value of the Roche limit, expressed using the average density of satellites, is slightly smaller than that of Eq. (21). By the way, some explanations (e.g. Wikipedia) use a coefficient of 2.423, which is a little smaller than the value above, but it is an approximation calculated assuming that the shape of the satellite is a simple prolate spheroid.
Since a real satellite is neither as soft as a fluid nor as hard as a rigid body, it will break somewhere between the fluid limit and the rigid limit. Phobos is already inside the fluid limit and is expected to break in a few tens of millions of years. I would love to see Mars with rings.
I wanted to see how bumpy the ocean tides are, so I made animations showing tides near the equator.
For the data, I used the ocean tide model of the National Astronomical Observatory of Japan.
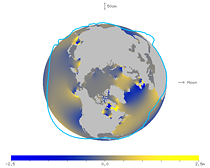
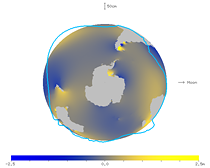
The figures below emphasize the tide level of the M2 constituent averaged between 15 ° N and 15 ° S.
If you look carefully, you can see that the tide tends to swell up at a point well off to the east from the direction of the moon.
In the figures, the solid earth is also deformed vertically (+15 cm toward the moon and −15 cm at 90° from the moon) at the same scale as the ocean.
Though the solid earth deforms a little in the horizontal direction, it is neglected.
In this way, the actual tidal deformation seems to be quite different from the illustration in the textbooks.
 |
 |
| Fig. 25. Animation of the tides near the equator (viewed from the north). | Fig. 26. Animation of the tides near the equator (viewed from the south). |
The figures below show the spherical harmonic component of degree 2 and order 2 for the M2 constituent of the ocean tide, on the solid earth tide. Thus, averaging the ocean tide results in a smooth bulge with an amplitude of about 10 cm.
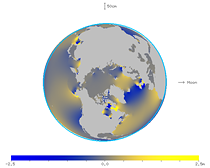 |
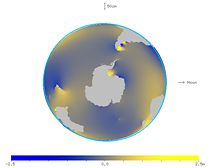 |
| Fig. 27. Animation of the spherical harmonic component of the ocean tide (viewed from the north). | Fig. 28. Animation of the spherical harmonic component of the ocean tide (viewed from the south). |
I also made animations of the tides seen in the frame on the earth's rotation. The figures below show the tide level of the M2 constituent near the equator. The two small yellow circles ● denote the direction of the moon and its opposite direction. You can see that the ocean responds with a long delay.
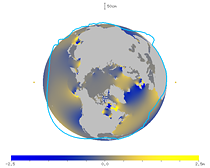 |
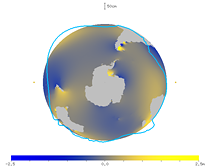 |
| Fig. 29. Animation of the tides near the equator (viewed from the north). | Fig. 30. Animation of the tides near the equator (viewed from the south). |
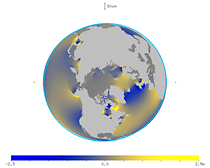 |
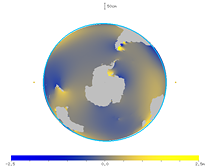 |
| Fig. 31. Animation of the spherical harmonic component of the ocean tide (viewed from the north). | Fig. 32. Animation of the spherical harmonic component of the ocean tide (viewed from the south). |
In this article, I have shown that the tidal force is a force due to the non-uniformity of gravity, i.e., it is the difference between the gravity acting at each point of the earth and the gravity acting at the center of the earth. Instead of taking the difference from the gravity at the center of the earth, we can add the opposite force, the translational inertial force. When tidal force is explained as a resultant force of forces in this way, the force to be added to the gravity at each point should be the translational inertial force, not the centrifugal force appearing in a rotating frame. In fact, even if we calculate the resultant force of the gravity and the centrifugal force around the common center of mass in a rotating frame, it will not be a tidal force. This is because when calculated in a rotating frame, a part of the centrifugal force centered on the common center of mass is added to the tidal force as the centrifugal force centered on the earth. Thus, the explanation of "the resultant force of gravity and centrifugal force" is clearly wrong.
Many textbooks and explanatory articles say, "When calculating the tidal force, we consider the revolution of the earth without rotation. In this case, the centrifugal force due to the earth's revolution is equal in magnitude and direction everywhere". It seems that the authors want to insist that the "centrifugal force due to revolution" is a special kind of centrifugal force that is equal everywhere, different from the usual centrifugal force that is proportional to the distance from the axis of rotation. However, since the earth is not rotating (i.e. not changing its orientation) in this case, the inertial force appearing on the earth cannot be a centrifugal force. In fact, as is known in the mechanics of a rigid body, this force is the usual uniform inertial force that appears due to translational accelerated motion, i.e., translational inertial force. There are not two types of centrifugal forces, but simply translational inertial force is mistaken for centrifugal force. In this way, many textbooks and explanatory articles misunderstand the definition of centrifugal force. Those who think it is centrifugal force probably forget that the earth is a rigid body and misunderstand circular motion (translational motion along a circle) as rotational motion. For a rigid body, circular motion and rotational motion are different, so the term "rotation" must be used very carefully.
Translational inertial force also appears in a rotating frame. Centrifugal force appears in a rotating frame around the common center of mass, and this centrifugal force can be decomposed into centrifugal force around the earth and translational inertial force. (Generally, in a rotating frame, translational inertial force appears in addition to centrifugal force when the axis of rotation is moved from the common center of mass to another position.) Tidal force can be expressed as the resultant force of this translational inertial force and gravity. This translational inertial force should not be called centrifugal force just because it appeared as a component of the original centrifugal force. Matsuda (2015) described this translational inertial force as "this component of the centrifugal force," but it should be written as the inertial force.
The misuse of "centrifugal force" in school education seems to have continued for a long time. This is because most experts of oceanography still refer to translational inertial force as "centrifugal force of equal magnitude and direction." Since the rotation of the earth is not assumed, the inertial force appearing on the earth cannot be a centrifugal force. However, in the field of oceanography, it seems to be believed that this force can be called "centrifugal force of equal magnitude and direction." As a result, educators may call translational inertial force "centrifugal force" without any doubt. For experts, there may be no inconvenience even if the terminology is used incorrectly, since the calculations can be performed without any problem. However, those who are explained by "centrifugal force" understand it as the original centrifugal force appearing in a rotating frame. They would never imagine that "centrifugal force" is used in the sense of translational inertial force. The meaning of "centrifugal force" in earth science differs from that in physics. In this way, confusion is occurring in the school education.
Extending the definition of "centrifugal force" in one field of study is a big problem both academically and educationally. The term "centrifugal force" used in tidal force should be changed to "inertial force" as soon as possible. In fact, some overseas sites (e.g., NOAA) explain tidal force using "inertial force" instead of "centrifugal force. Researchers and educators who are aware that centrifugal force is a mistake should speak up and correct the ongoing mistakes in educational and public institutions. Some may say that "centrifugal force" is easier to explain to high school students than "inertial force," but this should not be an excuse for teaching a mistake. Those who do not understand why centrifugal force is wrong, please read a physics textbook (e.g. Landau-Lifshitz) and study the mechanics of a rigid body.
Then, how should we explain tidal force? "Tidal force is the difference between the gravity of the moon at each point of the earth and the gravity of the moon acting at the center of the earth" is a correct explanation, but you may not feel that you understand it only by this. I think that the following is better: "Tidal force is the resultant force of the moon's gravity acting on each point of the earth and the inertial force acting uniformly on the entire earth due to the accelerated motion toward the moon. The gravitational and inertial forces just cancel each other at the center of the earth, but remain uncanceled at each point on the earth because the gravity varies from place to place." In terms of content, instead of taking the difference, we are just adding the force in the opposite direction. By the way, this explanation is basically the same as that of the tidal force acting on a free-falling elevator.
(Addendum: "Centrifugal force" has its roots in G.H. Darwin? 2021/07)
In researching the roots of the expression "centrifugal forces of equal magnitude and direction," I came across a late 19th century book entitled "The tides and kindred phenomena in the solar system" (1898) by George H. Darwin (son of Charles Darwin).
G.H. Darwin was an astronomer who developed the theory of tidal acceleration of the moon and was a leading authority on the theory of tides.
The above book was the one for the general public, written by Darwin.
The book seems to have been well received and is still being reprinted more than 100 years after its publication.
In this book, Darwin employed an ideal model of an earth that has stopped rotation and "equal and parallel centrifugal forces" acting on the earth to explain tidal forces in an easy-to-understand manner.
Instead of "translational inertial force," which is difficult for ordinary people to understand, the term "centrifugal force" may have been used to mean inertial force in general.
Unfortunately, however, the definition of centrifugal force cannot be extended to translational inertial force.
In truth, he should have written "inertial forces of equal magnitude and direction."
Darwin's fame is astonishing that his books are still being reprinted, but it would be ironic if the misuse of "centrifugal force" has continued for more than 100 years because of his fame.
By the way, Darwin wrote a detailed article on tides in the "Encyclopedia Britannica" for specialists, including the most advanced topics of the time. He wrote there that tidal force is "the difference between the gravity acting at each point of the earth and the gravity at the center of the earth," and he never used the word "centrifugal force." This suggests that Darwin may have used "centrifugal force" for the general public, knowing the misuse of the term, where he should have used "inertial force." In other words, the term "parallel" centrifugal force would have been substituted for inertial force. The truth may be that other experts have been using the "parallel" centrifugal force for more than 100 years without realizing that they were misusing it. ( → G.H. Darwin - Amendments )
In Japan, tidal force used to be taught as the difference between the gravity acting at each point of the earth and the gravity acting at the center of the earth. However, it was difficult for teachers to explain why high tides occur on both sides of the earth. Then, Darwin's "equal and parallel centrifugal forces" was introduced to school education in the 1960s and was welcomed by teachers. As a result, the misunderstanding that translational inertial force due to revolution could be called centrifugal force has spread... In the United States, tidal force has been taught using inertial force for many years. Japan should get rid of this misunderstanding as soon as possible.