潮汐力を遠心力で説明してはいけない
— 潮汐力の正しい理解のために —
2021年1月 藤原隆男
|
要旨
学校教育でも使われている「潮汐力は月による重力*と地球の公転による遠心力との合力である」という説明は間違っている。 なぜなら,
-
「遠心力」を文字通り「地球の公転運動による共通重心周りの遠心力」の意味で使っていたら …
間違い。公転運動に乗った回転系で重力と遠心力の合力を計算すると, [潮汐力]+[地球中心周りの遠心力] になる。
地球中心周りの遠心力 (潮汐力の 41 倍もある) を差し引かないと潮汐力にはならない。
このように, 本来の遠心力を使うと潮汐力を正しく求めることができない。
-
「遠心力」を「大きさと向きが等しい遠心力」として使っていたら …
遠心力ではない力を誤って遠心力と呼んでいる。
地学の教科書**が陥っている間違いだ。
潮汐力を求めるときは, 上述の [地球中心周りの遠心力] が現れないよう, 地球の回転を止めて公転だけを考える。
回転を止めた公転運動は並進運動であって, これを回転運動と呼ぶのは誤りだ。
また, 地球は回転していないので, 地球に現れる慣性力は遠心力ではありえない。
この慣性力は, 月に引かれることによる地球の並進加速度運動で出てくるふつうの一様な慣性力 (並進慣性力) だ。
これを遠心力と呼んではいけない。
遠心力は, 大きさが回転軸からの距離に比例し, 外向きにはたらく放射状の力のことなので, 大きさと向きが等しい力はそもそも遠心力の定義と矛盾する。
じつは, 潮汐力は, 場所による重力の差に起因する力で, 大きさのあるものが重力を受けるだけで出てくる。
地球が月に向かって直線運動していてもはたらく。
回転運動や遠心力は, 潮汐力とは関係ない。
合力で説明するなら,
「潮汐力は, 月の重力と, 地球が月に引かれることで地球全体に一様にはたらく慣性力との合力である」が正しい。
一様な慣性力とちょうど逆の力が地球の中心にはたらく月の重力なので,
「潮汐力は, 地球の各点にはたらく月の重力と, 地球の中心にはたらく月の重力との差である」 でもよい。
「遠心力」は用語の誤用なので,
教科書や解説書の「遠心力」を「慣性力」に書き直すべきだ。
また, 大学入試で潮汐力がしばしば出題されているが, 潮汐力が正しく教えられていない現状では出題を控えるべきだろう。
ちなみに, 日本天文学会の天文学辞典は, 潮汐力を天体からの重力の差で説明している。
また, 気象庁は, さいきん潮汐力の説明文中の「回転」を「公転」に, 「遠心力」を「慣性力」に改めた (2021年12月)。,
* 教科書は,地球による地表での重力を「重力」, 月などの天体による重力を「引力」とよんでいるが,ここでは物理学にしたがってどちらも「重力」とよぶことにする。
** 高校地学の教科書でも, 潮汐力の説明から遠心力が消え, 潮汐力が重力の差として説明されるようになった (2023年4月)。
予備知識
大きさをもたない質点では, 円運動している質点を考えるとき回転系に乗るのがふつうなので,
円運動と回転運動を同一視してもかまわない。
しかし, 大きさをもつ剛体には向きがあるので, 並進円運動
(円に沿った並進運動) と回転運動をちゃんと区別しなければならない。
すなわち, 並進運動 (translation) とは慣性系に対して向きを変えない運動のこと,
回転運動 (rotation) とは慣性系に対してある軸を中心に向きを変える運動のことだ。
潮汐力を正しく理解するためには, まず地球が大きさをもつ剛体であることを認識する必要がある。
そして, 下表に示したように, 剛体の運動には並進運動と回転運動があること,
並進運動と回転運動では剛体の座標系に現れる慣性力 (見かけの力) の場が異なることを知っておかなければならない。
すなわち, 並進加速度系では一様な慣性力の場 (並進慣性力) が現れる。
いっぽう, 回転系では回転軸から外向きにはたらく放射状の慣性力の場 (遠心力) が現れる。
地球中心での並進慣性力と遠心力が等しいからといって, これらを混同してはならない。
表. 座標系による慣性力の分類
剛体の運動
(剛体が乗る座標系) |
慣性力の種類 |
並進加速度運動
(並進加速度系) |
並進慣性力 … ふつうの慣性力, すなわち一様な (どこでも大きさと向きが等しい) 慣性力。 |
回転運動
(回転系) |
遠心力 … 大きさが回転軸からの距離に比例する外向きの力。
(注)
遠心力のほか, 座標系に対して運動する質点には「コリオリ力」がはたらく。
また, 角速度が変化するときは「オイラー力」(横慣性力) が現れる。
|
 |
 |
| 並進円運動 (回転運動ではない) |
並進慣性力 (遠心力ではない) |
 |
 |
回転運動
|
遠心力
|
| * 図中の G は地球と月の共通重心 |
|
はじめに
潮汐力の説明として「潮汐力は月による重力と地球の公転による遠心力との合力である」という表現がよく使われる。
地球の公転とは, 地球と月の共通重心の周りの公転運動のことだ。
じっさい, 高校の地学の教科書では, 潮汐力は重力と遠心力の合力として説明されている
(その後改訂 - 追記 9 参照)。
また, ウェブで検索してみると, 気象庁の
「潮汐の仕組み」
でも潮汐力を同じように説明している
(その後改訂 - 追記 3 参照)。
この説明を学校で習って, そのまま信じている人も多いだろう。
ところが, じつはこの説明は間違いだ。
そもそも潮汐力に回転運動や遠心力は必要ない。
また, 教科書で「遠心力」と呼ばれている力は, 遠心力ではなく並進慣性力または一様慣性力という別の力だ。
潮汐力の説明に遠心力を使うことの問題点は, 1990年代から物理系の研究者によってたびたび指摘されている
[恒岡 (1993), 斎藤 (2007), Butikov (2017)]。
とくに, 筆者と同じ宇宙物理の 松田卓也 氏は論文 (2009) や書籍 (2014) で注意を喚起しておられる。
筆者も, 遠心力が潮汐力と関係ないことは知っていたが, 数年前に松田氏の論文を読んで問題の奥深さがわかってきた。
多くの地球科学や天文学の専門家が, 潮汐力の説明の間違いに気付いていないのだ。
じっさい, ウェブで専門家の解説や大学の講義資料を見てみると, ほとんどが遠心力を使った間違った説明をしている。
そこで, 本稿では潮汐力についての誤解の原因を考察し, 正しい説明を試みる。
本稿が, 教科書やウェブ上で見られる誤った説明を正していく一助になればさいわいである。
(追記 1) 潮汐力を正しく理解するための基本である「剛体の運動」と「慣性力」について
補足: 剛体の運動と慣性力
にまとめておいたので参考にされたい。
専門家でも潮汐力の説明を間違えるのは, 剛体の運動 (並進運動と回転運動) を理解していなかったり, 「遠心力」の定義を誤解していたり, 「並進慣性力」を知らなかったりするのが原因ではないかと思われる。
潮汐力にまつわる誤解を解消するために, まずこの補足を読んでほしい。
とくに, 剛体では円運動 (並進円運動) と回転運動は別の運動なので, これらを混同してはならない。
また, 地球中心での大きさが一致するからといって, 並進慣性力と遠心力を混同してはならない。
(2021年3月)
(追記 2) 地球-月系に現れる慣性力を表す アニメーション
を作成したので参考にされたい。
(2021年6月)
(追記 3) 気象庁が「潮汐の仕組み」ページの「回転」を「公転」に,
「遠心力」を「慣性力」に書き換えたようだ。すばらしい。
気象庁に間違いを指摘してくださった三宅唯先生, ありがとうございます。
以下, 気象庁による注:
『当ページでは従来これを「遠心力」と表記しておりましたが、正確な表現とするため「慣性力」にあらためました。』
また, 「潮汐・海面水位の知識 用語集」でも, 起潮力 (潮汐力) の説明が慣性力を使ったものに変わっている:
「潮汐を起こす力のこと。月や太陽が地球に及ぼす引力は地球上の各点でわずかに異なる一方、地球の重心で引力と釣り合っている慣性力は地球全体で一律に作用するため、地球上では力の不均衡が生じ、これが起潮力となる。」
すばらしい。
(2021年12月)
(追記 4) ・過去の入試センター試験で潮汐力の求め方を問う出題が何度かあったことがわかったので,
不適切な大学入試問題 というコメントを掲載した。 (2022年1月)
・東京大学が前期入学試験物理の潮汐力を求める問題で, 慣性力と書くべきところを遠心力と書いてしまったので, コメントを追加した。 (2022年2月)
(追記 5) ・高校の 地学教科書 を入手したので, 大胆にも潮汐の部分を修正してみた。 (2022年2月)
・比較のため, 海外での潮汐力の説明 として, アメリカの例をいくつかあげた。
アメリカでは, すでに「慣性力」が使われている。
・太陽系力学の 大学生向けの教科書 C.D. Murray & S.F. Dermott: Solar System Dynamics (1999) も修正してみた。
・G.H. Darwin の古典的名著 The tides and kindred phenomena in the solar system (1898) も修正してみた。
(2022年2月)
・松田卓也氏の 間違いだらけの物理学 (2014) 4章 「『潮汐力の説明』の間違い」 も修正してみた。
(2022年10月)
(追記 6) ・国立天文台 RISE 月惑星探査プロジェクト が「遠心力」を「慣性力」に改訂。 対応をありがとうございます。 (2022年3月)
・日本測地学会が 「測地学テキスト」の 地球潮汐 での潮汐力の説明を「遠心力」から「慣性力」へ変更。 対応をありがとうございます。 (2022年3月)
(追記 7) ・教科書・百科事典が潮汐力 (起潮力) を正しく説明しているかどうか,
成績表 を付けてみた。 (2022年8月)
(追記 8) ・補足2:
加速度系における潮汐力の導出 を追加した。 (2022年8月)
(追記 9) ・2023年用 地学教科書:
高校の地学教科書が改訂。 潮汐力の説明から遠心力が消え, 潮汐力が重力の差として説明されるようになった。 (2023年4月)
(追記 10) ・1970-1980年代の地学教科書:
過去の高校地学教科書を調べたところ, 遠心力が使われるようになったのは 1980 年代であった。 (2025年2月)
第1部 潮汐力
潮汐力とアインシュタイン
日本天文学会天文学辞典の 「潮汐」 では潮汐力はつぎのように説明されている。
すなわち「天体の各部分にはたらく重力と天体の重心にはたらく重力との差のことを潮汐力と呼ぶ」。
じつに明快だ。
潮汐力の対象は天体でなくてもかまわない。
たとえば, 地球の重力に引かれて自由落下するエレベータにも潮汐力ははたらく。
これは, 重力の大きさや向きが場所によって異なるからだ。
エレベータの各点にはたらく重力は, 地球に近い側では強く, 遠い側では弱い。
また重力は地球の中心に向かうので, エレベータの側面では重力が斜め向きになる。
そこで重心にはたらく重力との差をとると, 図1の青い矢印のように, 地球の方向にはエレベータを引き伸ばそうとする力が, それと垂直な方向にはエレベータを押す力が残ることがわかる。
これが潮汐力だ。
このような小さい乗り物に現れる潮汐力は弱いと思うかもしれないが, それでも無視できない力だ。
たとえば, 国際宇宙ステーションもエレベータと同じように地球に向かって自由落下している (ただし, 地球にぶつからないよう秒速 7.7 kmで横へ逃げつづけている) ので内部は無重力に近いが, 周辺には潮汐力が残る。
国際宇宙ステーションは 100 メートルほどの大きさがあるので, 端の方ではそれなりの潮汐力が現れる。
計算してみると, 静止状態で浮かんでいるものを 10 分後には何十メートルも移動させるくらいの力だ。
 |
|
図1. 自由落下するエレベータの内部にはたらく単位質量あたりの力。
重心では重力と慣性力が打ち消し合うが, それ以外の場所では潮汐力が残る。
|
しかし, なぜ重心にはたらく重力との差をとるのか。
これには, 「慣性力」を思い出す必要がある。
質量には, 運動状態を維持しようとする性質, すなわち慣性がある。
この慣性のため, 加速度運動をするものに乗ると見かけの力が現れることになる。
これが慣性力だ。
たとえばバスが急発進するとき, バスに乗っている乗客は慣性があるのでその場所にとどまろうとする。
これをバスの中で見ると, 後ろ向きの力が現れて乗客が後ろへ引っ張られるように見える。
このように, 慣性力は, 慣性系 (静止系と等速直線運動する座標系をまとめて慣性系という) では見えず, 加速度系に乗ったときだけ現れる見かけの力だ。
上下運動のときも同様で, たとえばエレベータが降下を始めると, 上向きの慣性力が現れて一瞬からだが軽くなる。
とくに, 重力に身を任せて自由落下するときは, 重心での重力と同じ大きさで逆向きの一様な慣性力がエレベータ全体に現れ, 重心では力が打ち消しあって無重力になる。
このように, 重心にはたらく重力と逆向きの慣性力を加えること, つまり重心にはたらく重力との差をとることが, 自由落下するエレベータの内部で見える力を理解するためには自然なことだ。
じつは, 重力に身を任せて運動すると重力が消えることに目を付けたのがアインシュタインだ。
アインシュタインは, 重力を消すことができるのは重力と慣性力の根源が同じためだと考え, 一般相対性理論を作った。
また, 重力が消えた空間 (自由落下運動する座標系) を局所慣性系と呼んだ。
重力がなくなると, 力を受けない空間すなわち慣性系になる。
自由落下するエレベータの中は, 地球から遠く離れた空間と同じ慣性系で, 基準とするべき座標系はこちらの方というわけだ。
「局所」という語を付けたのは, 無重力にできるのが重心だけで, その周辺では重力の非一様性のために一部の重力が残ってしまうからだ。この消えずに残った重力が潮汐力だ。
ちなみに, 国際宇宙ステーションの環境も, 無視できない潮汐力があるので, 無重力環境ではなく微小重力環境と呼ばれている。
図2は, 自由落下のアニメーションだ。
エレベータの代わりに球殻状にテスト粒子を配置して手を離し, それらの粒子が天体 (黄色い円) からの重力で落下するようすを示した。
テスト粒子は軽くて, お互いに重力で引き合うことはないとしている。
これを球殻の中心 (+) から見ると, 潮汐力によって球殻が引き伸ばされていくように見える (図2B)。
図2C には, 自由落下ではないが, 銀河遭遇のシミュレーション動画を載せておいた。
銀河の密度分布を仮定し, 星をテスト粒子として扱って計算を簡略化している。
われわれ天文屋は, このような動画をよく見ているので, 潮汐力は重力の差によって天体を変形させる力のことだと理解している。
自由落下するエレベータに働くのと同じ力だ。
図2からわかるように, 潮汐力は大きさをもつものが重力を受けるだけで現れる。
回転運動とは関係ない。
これを遠心力で説明されても「え?」となるのだ。
 |
 |
 |
| 図2. 自由落下する球殻のアニメーション。
球殻上の点は, それぞれ黄色い円に向かって落下しているだけだ。 |
図2B. 自由落下する球殻のアニメーション。
球殻の中心から見たところ。 |
図2C. 銀河遭遇に伴う銀河の潮汐変形のアニメーション |
非回転系で見た潮汐力
自由落下するエレベータを, 月に向かって「自由落下」する地球で置き換えたのが図3だ。
地球に乗って見ると, 月に向かう加速度運動のため地球全体に一様な慣性力がはたらく。
慣性力の大きさは地球の中心での月による重力と等しく, 向きは重力と逆だ。
時計回りに 90° 回せば図1とほとんど同じになる。
* この解説では, 簡単のため月による潮汐力だけを考えることにする。
実際には, 地球は太陽による潮汐力も受ける。 その大きさは月の潮汐力の約 0.46 倍だ。
 |
|
図3. 地球の各点にはたらく月の重力 (水色) と地球全体に一様にはたらく慣性力 (ピンク) を足すと 潮汐力 (青) が残る。
地球の中心では重力と慣性力がちょうど打ち消し合う。
|
エレベータとの違いは, 地球と月が互いにぶつからないように横によける運動, いわゆる公転をしていることだ。
質量の比から計算すると, 地球と月の共通重心は地球の内部にあり, 地球と月はこの共通重心のまわりを公転していることになる。
(共通重心が地球の内部にあることは, これからの議論には本質的ではない。)
地球の公転運動を入れて描き直したのが図4だ。
簡単のため円軌道を仮定している。
また, 図3と同様に地球の自転を止めて考えている (というか, 地球の余計な運動を考えていない)。
地球の運動方向がしだいに月の方へ曲がるのは, もちろん月による重力のためだ。
このように, 図3と比べて横へよけながら落ちているという違いはあるが, 地球が月に向かって加速度運動することによって, 地球から見ると一様な慣性力が現れることに変わりはない。
この一様な慣性力を, 慣性力全般と区別するため, 並進加速度運動に起因する慣性力という意味で「並進慣性力」と呼ぶことがある。
ここでも, この用語を使うことにしよう。
 |
|
図4. 月に引かれることによる地球の並進加速度運動, すなわち共通重心 G のまわりの並進円運動のため, 地球に乗って見ると, 地球全体に一様にはたらく慣性力 (遠心力ではない!) が現れる。
|
この一様な慣性力 (並進慣性力) を「遠心力」と呼ぶ人がいる (ほとんどの教科書もそうだ) が, それは間違いだ。
なぜなら, 地球は慣性系に対して回転していないからだ
(回転とは, 向きを変える運動のこと)。
回転系ではないので, この慣性力は遠心力ではありえない。
地球は, 向きを変えず, ただ円に沿った並進加速度運動をしているだけだ。
並進加速度運動をしている地球に現れる力は, 自由落下するエレベータの内部と同じ並進慣性力のはずだ。
図4の慣性力の大きさがどこでも同じになるのは地球の各点が同じ半径の円運動をしているからだ, という説明もよく見かける
(たとえば
広島大学 自然システム教育学研究室
ではアニメーションまで使って説明している)。
しかし, 地球をいくつかの円運動する点に分ける説明は, 誤解を招きやすい。
じっさい, 多くの人が各点の並進円運動を回転運動と勘違いし, 並進慣性力を遠心力と間違えている。
大学生向けの教科書 Solar System Dynamics (2000) まで, 並進慣性力のことを「大きさと向きが等しい遠心力」と書いている。
慣性力の大きさと向きがどこでも等しいのは, 単に地球が剛体として並進加速度運動をしているからだ。
剛体の並進加速度運動では, すべての点が慣性系に対して同じ運動をするので, どこでも同じ慣性力が現れるのは当然なのだ。
繰り返しになるが, この慣性力は並進運動による慣性力であって, 回転運動による慣性力ではないので, これを遠心力と呼んではいけない。
(→ 並進円運動と回転運動の違い, 並進慣性力と遠心力の違いについては
補足: 剛体の運動と慣性力 参照。)
 |
|
図5. 地球の中心を原点とする座標系
|
ここで, 少し式を使ってみよう。
大学1年程度の物理しか使っていないので, 理系の人にとって理解は容易だろう。
簡単のため, まず月の方向だけを考えることにする。
図5のように, 地球の中心を原点とし, 地上の点の月方向への距離を \( x \),
月までの距離を \( a \) とする。
また, 月の質量を \( m \) ,
重力定数を \( G \) とすると,
地上の点が月から受ける単位質量あたりの重力
\( f \) は, 月までの距離の2乗に反比例する。
\( x \) が
\( a \) に比べて十分小さいとき,
\( f \) はつぎの式で近似できる。
\[
f = \frac{{Gm}}{{{(a - x)}^2}} \approx \frac{{Gm}}{{a^2}} + \frac{{2Gm}}{{a^3}}x. \tag{1}
\]
右辺の第1項は, 地球全体が月から受ける一様な重力, あるいは地球中心での月の重力を表す。
第2項は, 地上の点と地球中心での月の重力の差, すなわち潮汐力だ。
この力 \( f \)
は, もちろん慣性系から見たときの月の重力だ。
これを月に引かれて加速度運動する地球から見ると,
地球中心での月の重力が逆向きの慣性力と打ち消し合う結果, 潮汐力だけが残ることになる。
地球から見たときの力を
\( f' \) とすると, これは上式の
\( f \) と一様な慣性力 \( -Gm/{a^2} \) の合力として表すことができる。
すなわち,
\[
f' = \frac{{Gm}}{{{(a - x)}^2}} - \frac{{Gm}}{{{a^2}}} \approx \frac{{2Gm}}{{{a^3}}}x. \tag{2}
\]
これが, 月方向での潮汐力 (単位質量あたり) の式だ。
このように, 潮汐力は月の重力と一様な慣性力の合力, あるいは地球上の点における月の重力と地球中心における月の重力の差で表すことができる。
月に近い側では月の重力が慣性力を上回るので月方向の力が残り, 月と反対の側では慣性力が上回るので月と反対向きの力が残るというわけだ。
潮汐力が地球の公転運動と関係なく出てくることに気をつけてほしい。
潮汐力は地球が重力を受けて加速度運動するだけで出てくる力なので, 地球がどんな運動をしていてもかまわないのだ。
地球が月に正面から向かっていても, 瞬間的に静止しても, 潮汐力は現れる。
上式では\( x \)方向だけを考えた。
こんどは, 3次元での潮汐力を計算してみよう。
あとで潮汐力による等ポテンシャル面の変化を調べるため, 地球自身の重力も含めることにする。
まず, 慣性系で考えよう。
図5のように, 地球の中心を原点とし, 月の方向を \( x \),
月の進行方向を \( y \),
北を \( z \),
月までの距離を \( a \) とする。
また, 地球の質量を \( M \),
月の質量を \( m \) とし,
重力定数を \( G \) とする。
地球各点の単位質量あたりのポテンシャルエネルギーを \( V \)
とすると, これは地球自身による重力ポテンシャルと月による重力ポテンシャルとの和になる。
すなわち,
\[
V = - \frac{GM}{\sqrt {{x^2} + {y^2} + {z^2}} } - \frac{Gm}{\sqrt
{{{(x - a)}^2} + {y^2} + {z^2}} } . \tag{3}
\]
力の代わりにポテンシャルを使ったのは, ポテンシャルのほうが式が簡潔になるからだ。
力を使うと, ベクトル式または成分に分けた式を書かないといけないので煩雑になる。
なお, ポテンシャルの定義より, 力の式はポテンシャルの式を座標方向に微分して符号を変えることで得られる。
たとえばポテンシャルを \( x \) で微分して符号を変えると力の
\( x \) 成分が出てくる。
式 (3) の第2項は月による重力ポテンシャルだ。
これを \( V_{\rm{m}} \) とおき,
\( x, y, z \) が
\( a \)
と比べて十分小さいとして
\( x, y, z \) の2次の項まで展開すると, つぎの式で近似できることがわかる。
\[
\begin{eqnarray}
{V_{\rm{m}}} &=& - \frac{{Gm}}{{\sqrt {{{(x - a)}^2} +
{y^2} + {z^2}} }}\\ &\approx& - \frac{{Gm}}{a} -
\frac{{Gm}}{{{a^2}}}x - \frac{{Gm}}{{{a^3}}}({x^2} - {\textstyle{1
\over 2}}{y^2} - {\textstyle{1 \over 2}}{z^2}) . \tag{4}
\end{eqnarray}
\]
最初の項は定数なので無視してよい。
第2項は地球全体が月から受ける一様な重力, あるいは地球の中心にはたらく月の重力を表す。
第3項は潮汐力, あるいは地上各点での月の重力の, 地球中心での月の重力からのずれを表す。
(この式は, ルジャンドル多項式を用いて求めることもできる。)
ここで, 月に引かれて加速度運動する地球の座標系に移ろう。
加速度系で見ると, エレベータの内部と同じように並進慣性力が現れる。
この慣性力は, 式 (4) の第2項が表す地球中心での月の重力と大きさが同じで向きが逆だ。
したがって, 加速度系で見ると式 (4) の第2項は打ち消し合ってなくなる。
けっきょく, 地球から見ると, 地球自身の重力と月による潮汐力だけが残る。
こうして, 加速度系での力を表すポテンシャル \( V' \) は, 定数項を除いてつぎの式で近似できることになる
(運動方程式を用いたポテンシャルの導出は
補足2: 加速度系における潮汐力の導出 を参照)。
\[
\begin{eqnarray}
V' \approx - \frac{{GM}}{{\sqrt {{x^2} + {y^2} + {z^2}} }}
- \frac{{Gm}}{{{a^3}}}\left( {{x^2} - \tfrac{1}{2}{y^2} - \tfrac{1}{2}{z^2}} \right) . \tag{5}
\end{eqnarray}
\]
この式の第2項を微分することで単位質量あたりの潮汐力の大きさ, つまり潮汐加速度を求めることができる。
いま, 潮汐加速度を \( \boldsymbol{f}' \) と書くと,
月の方向の潮汐加速度は \( f'_{x} = 2Gmx/{a^3} \),
月と垂直な方向の潮汐加速度は \( f'_{y} = -Gmy/{a^3} \) となる。
これを用いて計算した潮汐力の大きさが図6の数値だ。
地表での重力加速度 9.8 m/s2
と比べると, 月の方向での潮汐加速度はその約1千万分の1, 月と垂直な方向での潮汐加速度はさらにその半分であることがわかる。
 |
|
図6. 地球の各点にはたらく単位質量あたりの力。
月の反対側, 地球の中心, 月に近い側 からの月までの距離の比はおよそ 61:60:59
なので, 重力 (水色) の大きさの比はおよそ 29:30:31 となる。
このうち中心での重力を逆向きにしたのが並進慣性力 (ピンク) だ。
潮汐力 (青) は, 重力や並進慣性力に比べてずいぶん小さいことがわかるだろう。
|
つぎに, 潮汐力による等ポテンシャル面の変位を求めてみよう。
地球の半径を \( R \),
潮汐力による月方向での等ポテンシャル面の上昇分を \( \zeta \) とする。
上昇した等ポテンシャル面での重力ポテンシャルと潮汐ポテンシャルの和は, 式 (5) で \( x = R+\zeta \) と置くと出てくる。
\( \zeta \) が \( R \)
と比べて十分小さいとすると,
\[
V' \approx - \frac{{GM}}{{R + \zeta}} - \frac{{Gm}}{{{a^3}}}{R^2}
\approx - \frac{{GM}}{R} + \frac{{GM}}{{{R^2}}}\zeta - \frac{{Gm}}{{{a^3}}}{R^2}. \tag{6}
\]
等ポテンシャル面の上昇による潮汐ポテンシャル (最後の項) の変化分は, 十分小さいので無視した。
式 (6) が, 潮汐力がないときのポテンシャル \( -GM/R \) と等しいことより,
月方向での等ポテンシャル面の上昇はつぎのようになる。
\[
\zeta = \left( {\frac{m}{M}} \right){\left( {\frac{R}{a}} \right)^3}R. \tag{7}
\]
同様にして, 月と垂直な方向ではつぎの式で書ける。
\[
\zeta = - \frac{1}{2}\left( {\frac{m}{M}} \right){\left( {\frac{R}{a}} \right)^3}R. \tag{8}
\]
これを数値で表すと, 月の方向では +0.36 m, 月と垂直な方向では −0.18 m になる。
高低差 54 cm, 平均 ± 27 cm。 これが, 月による潮汐力の大きさだ。
図7には, 地表のいろいろな点での潮汐力の向きと大きさを示しておいた。
Wikipedia の英語ページにも
同じような図 が出ているが, 図が不正確 (2021年1月現在) なので気をつけてほしい
(比較: 筆者による修正版)。
参考までに, 図7の矢印の先を滑らかな線で結ぶと楕円になる。矢印の先が正確な楕円になっていない図は, いいかげんに描いた図と思ってよい。
 |
|
図7. 地球の各点にはたらく潮汐力
|
また, 潮汐力の図に潮汐ポテンシャル (式 (5) の第2項) の等高線を重ねると, つぎのような図が描ける。
 |
|
図7'. 地球周辺の潮汐ポテンシャル
|
回転系で見た潮汐力
以上で見てきたように, 潮汐力の説明に回転運動は必要ない。
しかし, 図4のような並進座標系で見ると, 月や地球の位置が時間とともに変わり, 並進慣性力の向きもぐるぐると変わるので, 式 (3), (4), (5) は一瞬しか成り立たないことになる。
これを避けるためには, 公転とともに回る回転系に乗るとよい。
地球は, こんどは回転系に対して止まっていると仮定する。
そうすると, コリオリ力のような余計な見かけの力が現れないだけでなく, 地球の各点にはたらく力の時間変動もなくなるので, 理解が容易になる。
ところで, 回転系で見ると見かけの力である遠心力が必ず現れる。
遠心力は, 回転軸を中心として外向きにはたらく力で, 大きさは回転軸からの距離に比例する。
地球を北側から見ると, 共通重心の周りの遠心力のようすは図8のようになる。
教科書は,「潮汐力は月による重力と共通重心の周りの遠心力との合力」というが, 月の重力とこの遠心力を合わせても潮汐力にならないことは, 図3と見比べると明らかだろう。
じっさい, たとえば月方向での合力の大きさを計算すると 46.4×10−6 m/s2, すなわち図6の潮汐力の 42 倍になってしまう*。
これは, 潮汐力に,その 41 倍もある地球中心の遠心力が加わるためだ
(地球と月の質量比を 81 とすると, 地球中心の遠心力は潮汐力の (81+1)/2 = 41 倍になる, 式 (14') 参照)。
つまり, 教科書の説明どおり正直に合力を計算しても, 潮汐力にならないのだ。
月による重力との合力の相手は, 遠心力ではなく図3のピンクの矢印で表される慣性力でなければならない。
では, 回転系に乗って見たとき, この慣性力はどこから出てくるのだろう?
* 月と反対側でも,合力の大きさは同じで方向は逆になる。松田卓也氏は著書で, 月の側とその反対側では合力の大きさが異なると述べているが, それは松田氏の早合点だ。
 |
|
図8. 回転系で共通重心の周りに現れる遠心力
|
また少し式を使おう。
共通重心を原点とする座標系を使うのが自然かもしれないが, 知りたいのは地球の中心から見た力なので, 図5と同じ座標系を使うことにする。
ただし, こんどは座標系が地球-月系とともに回転すると仮定しているので, 月や地球は回転系に対して静止している。
ところで, 回転系に乗ると, 必ず見かけの力である遠心力が現れる。
遠心力は回転軸と垂直な方向に放射状にはたらく力で, その大きさは回転軸からの距離に比例するという特徴がある。
これは, 回転軸からの距離の2乗に比例するポテンシャルで表現することができる。
けっきょく, 回転系におけるポテンシャルは, 地球 (質量\( M \)) の重力によるポテンシャルと月
(質量\( m \)) の重力によるポテンシャルと遠心力によるポテンシャルの和になる。
すなわち,
\[
V = - \frac{{GM}}{{\sqrt {{x^2} + {y^2} + {z^2}} }} -
\frac{{Gm}}{{\sqrt {{{(x - a)}^2} + {y^2} + {z^2}} }} -
\frac{1}{2}{\Omega ^2}[{(x - {x_{\rm{G}}})^2} + {y^2}] . \tag{9}
\]
第2項は月による重力ポテンシャル, 第3項は遠心力ポテンシャルだ。
このうち, 月による重力ポテンシャルが式 (4) のように近似できることはすでに述べた。
いっぽう, 遠心力ポテンシャルは, 回転軸からの距離の2乗に比例する。
いま, 遠心力ポテンシャルを
\( V_{\rm{c}} \) とすると,
\[
{V_{\rm{c}}} = - \frac{1}{2}{\Omega ^2}[{(x - {x_{\rm{G}}})^2} +
{y^2}] . \tag{10}
\]
ただし,
\[
{\Omega ^2} = \frac{G(M + m)}{{a^3}}, \tag{11}
\]
\[
{x_{\rm{G}}} = \frac{m}{{M + m}}a. \tag{12}
\]
ここで \( {\Omega} \) は公転の角速度だ。
式(10)を展開し, 式(11)と式(12)を使って書き換えると, 遠心力ポテンシャルはつぎのように書けることがわかる。
\[
\begin{eqnarray}
{V_{\rm{c}}} &=& - \frac{1}{2}{\Omega ^2}({x^2} -
2{x_{\rm{G}}}x + {x_{\rm{G}}}^2 + {y^2})\\ &=&
\frac{{Gm}}{{{a^2}}}x - \frac{1}{2}{\Omega ^2}({x^2} + {y^2}) -
\frac{1}{2}{\Omega ^2}{x_{\rm{G}}}^2. \tag{13}
\end{eqnarray}
\]
上の2行目の式で, 第1項は一様な慣性力つまり並進慣性力を, 第2項は地球を中心とする遠心力を表す。
つまり, 共通重心の周りの遠心力は, 並進慣性力と地球中心周りの遠心力に分けることができるということだ。
第3項は定数なので無視してよい。
このポテンシャルを微分して符号を変えると, 図9 のような力の場が得られる。
 |
|
図9. 共通重心の周りの遠心力 (赤) は, 並進慣性力 (ピンク) と地球を中心とする遠心力 (黄) に分けることができる
|
けっきょく, 式(4)の \(V_{\rm{m}}\) すなわち月による重力と
式(13)の \(V_{\rm{c}}\) すなわち共通重心の周りの遠心力を加えた力は, 地球の中心にはたらく月の重力 (式(4)の第2項) と地球の公転運動による並進慣性力 (式(13)の第1項) が打ち消しあう結果,
\[
{V_{\rm{m}}} + {V_{\rm{c}}} \approx - \frac{Gm}{{a^3}}({x^2} -
{\textstyle{1 \over 2}}{y^2} - {\textstyle{1 \over 2}}{z^2}) -
\frac{1}{2}{\Omega ^2}({x^2} + {y^2}) + {\rm{const}}. \tag{14}
\]
または
\[
{V_{\rm{m}}} + {V_{\rm{c}}} \approx - \frac{Gm}{{a^3}}({x^2} -
{\textstyle{1 \over 2}}{y^2} - {\textstyle{1 \over 2}}{z^2}) -
\frac{1}{2}{\frac{G(M+m)}{{a^3}}}({x^2} + {y^2}) + {\rm{const}}. \tag{14'}
\]
という簡単な式になる。
右辺の第1項は潮汐力, 第2項は地球を中心とする遠心力だ。
このように, 回転系で見ると潮汐力のほかに必ず遠心力が現れる。
しかも, 遠心力の大きさは潮汐力よりも圧倒的に大きい
(月方向の潮汐力に対して \((M+m)/(2m)\) 倍, すなわち約 41 倍)。
こうして, 潮汐力を説明するときに回転系を使うと, 地球中心周りの大きい遠心力が現れて潮汐力を見えにくくしてしまう。
また, その遠心力がなぜ現れるか説明しなければならなくなる。
回転系に頼らずに潮汐力を説明するほうが賢明だろう。
ちなみに, この遠心力は周期27.3日の公転に乗った回転運動によるものだ。
地球を中心とする遠心力なので, 地球を公転面 (白道面) の全方向に膨らませようとするだけで, 潮汐には寄与しない。
実際の地球は, 公転に乗った回転系に対してさらに24時間50分という短い周期で (慣性系に対しては 23時間56分の周期で) 自転しているので, 赤道方向にかなり膨らんでいる。このような地球の回転による影響は, 潮汐力とは分けて考えるのがふつうだ。
地球を公転に合わせて回転させても, 並進慣性力が出てくることがわかった。
この並進慣性力と月の重力を合わせると, 潮汐力がちゃんと出てくる。
並進慣性力が重心周りの遠心力の分力として出てくるからといって, これを遠心力の平行成分 (たとえば 谷村) などと呼んではいけない。
並進慣性力という言葉があるのでそれを使うべきだ。
遠心力を回転軸以外の場所から見ると式 (13) のように並進慣性力が出てくることは, 力の場を矢印で表すとよくわかる。
図10は共通重心の周りの遠心力の場を z 軸方向から見たもので, 共通重心は G にある。
遠心力を軸方向から見るとこのように放射状に見える。
|
|
|
図10. 回転系で共通重心の周りに現れる遠心力の場。 G は共通重心。
(マウスオーバーまたはタップで地球を表示)
|
図10の遠心力場を2つの力に分けると, 並進慣性力 (図11) と地球を中心とする遠心力 (図12) になる。
これらの図は, 基本的には図9と同じだ。
ただ, 力を成分ごとに別々の図に分けて描いただけだ。
回転軸を地球の中心に移して考えるときは, このように2つの力に分ける方がわかりやすい。
図11と図12は, 式(13)の第1項と第2項にそれぞれ対応する。
図11と図12の力を重ねると図10の遠心力になることは容易に想像できるだろう (図10' 参照)。
また, 図11の力が「遠心力」でないことは明らかだ。
ちなみに, 回転軸を慣性中心 (共通重心) 以外の場所に移すと回転運動のほかに並進運動が現れることは, ランダウ=リフシッツの力学の教科書にも書いてある。
この並進運動に伴う力が並進慣性力だ。
|
|
|
| 図11. 共通重心の周りの遠心力を分解したときの, 地球全体に加わる並進慣性力。
(マウスオーバーまたはタップで地球を表示) |
図12. 共通重心の周りの遠心力を分解したときの, 地球中心周りの遠心力。 O は地球の中心。
(マウスオーバーまたはタップで地球を表示) |
回転中心ではない点で見た遠心力
並進慣性力と遠心力の関係を明らかにするための例として, 脱水機の中の洗濯物 (手袋のような小さいものがよい) を考えよう。
常識では, 洗濯物の水分が外へ離れていくのは強い遠心力が加わるからだ。
この描像は, 脱水機に乗って回転軸から見る限りは正しい。
しかし, 洗濯物にとっては事情が異なる。
前節で見てきたように, 遠心力を回転軸以外の場所すなわち洗濯物から見ると, 並進慣性力と洗濯物を中心とする遠心力に分けることができる。
遠心力をこのような2つの成分に分けて考えたとき, 洗濯物から水分を引き離そうとするのは, 主として並進慣性力の方だ。 洗濯物が小さいとき, 洗濯物を中心とする遠心力はマイナーな存在だ。
常識に反しているように聞こえるかもしれないが, 洗濯物の身になって考えると, 脱水の力は自分中心の遠心力ではなく並進慣性力であることがわかるだろう。
筆者自身は, 脱水機と似た乗り物に乗ったことがあるので, 遠心力が並進慣性力と自分中心の遠心力に分かれることは実感として理解できる。
それは, 2002年に JAXA との共同研究でフロリダのケネディ宇宙センターを訪れたときのことであった。
宇宙飛行士の殿堂という見学施設 (2015年に閉鎖されたようだ) に立ち寄ったら, 直径数メートルの回転アームの両端に人が乗るカプセルが付いた G-Force Trainer (YouTube)
という4G体験マシンがあった。
そこで勇気を出して乗ったわけだが, 外向けに押しつけられる力を予想して身構えていたところ, 回転が始まったとたんに回転椅子に乗せられてぐるぐる回されるような感覚が襲ってきた。
その後, 回転速度が一定になると回転椅子効果はおさまったが, 目が回る中で4Gの重力に耐えながら考えたのが回転椅子効果の原因であった。
そして気づいたのが, 回転運動を回転中心以外の場所で見ると, 並進運動と自分自身の回転運動に分けられるということであった。
その後者の効果で, 回転椅子に乗って回されるように感じたわけだ (実際には, 回転運動そのものよりも回転が加速するときに現れるオイラー力が効いて目が回ったと思われる…)。
いっぽう, 回転によって生じる外向きの4Gの力は, 乗っている人にとっては図11のような一様な力なのだ。
回転系に現れる遠心力を, 振り回される側に立って2つの成分に分けても, 向心力が機械による力の場合はあまり意味がないかもしれない。
しかし, 回転運動を起こす向心力が重力の場合は, 成分に分けることには意味がある。
なぜなら, 一様成分 (並進慣性力) が, 重力をほとんど消すという役割を果たすからだ。
実際, 宇宙ステーションのように重力に身を任せて運動するものに乗ると, 重力は慣性力でほとんど消えてしまう。
「ほとんど」と書いたのは, 消えずに残る力 (潮汐力や自分中心の遠心力) があるという意味だ。
ここまでの結論
潮汐力の単純で明解な説明は, 「地球の各点における月の重力と地球の中心における月の重力との差」だろう。
力の差をとる代わりに逆向きの力を足して, 「地球の各点にはたらく月の重力と地球の加速度運動によって地球全体にはたらく並進慣性力との合力」と説明してもよい。
このように, 潮汐力の説明に遠心力は必要ない。
教科書や多くの解説記事は, この並進慣性力を「大きさと向きが等しい遠心力」と間違って呼んでいる。
そもそも遠心力とは, 大きさが回転軸からの距離に比例する放射状の力のことだ。
「大きさと向きが等しい遠心力」などありえない。
並進慣性力を遠心力と勘違いするのは, 地球が剛体であることを忘れて, 円運動を回転運動と勘違いしていることが原因だと思われる。
地球の自転を止めた公転運動は並進運動なので, 地球に現れる力は並進慣性力であって遠心力ではない。
この並進慣性力を「遠心力」と呼ぶのは用語の誤用だ。
早急に「慣性力」と改めるべきだ。
また, 「遠心力」という語を使うことは, 回転系に乗っていることを宣言することになる。
つまり, 並進座標系で見える並進慣性力のつもりで不用意に「遠心力」を使うと, 意に反して回転系で見える本来の遠心力の意味になってしまうのだ。
このように, 「遠心力」の誤用は混乱を招くこと必至だ。
「遠心力」という語は, あたりまえのことだが, 本来の意味 (回転系に乗ると現れる, 回転軸からの距離に比例する放射状の力) でのみ使うべきだ。
第1部のおまけ
公転運動に乗った回転系では, 共通重心を中心とする遠心力が現れる。
この遠心力は, 並進慣性力と地球中心周りの遠心力に分けられるという話をした。
地球は回転系に乗っている, つまり慣性系に対して公転と同じ周期で回転していると仮定しているので, 地球中心周りの遠心力が現れるのは当然といえば当然だ。
それでは, 回転系に乗ったままで地球を公転と逆向きに回したら, つまり地球が慣性系に対して回転しないようにしたら, 地球中心周りの遠心力は消えるのではないか?
そう考える人もいるだろう。
筆者も一瞬そう思った。
しかし, 回転系に現れる遠心力は小細工をして消せるようなものではない。
では, 公転に乗った回転系に対して地球を逆向きに回したら何が起こるのか?
答えは, 「逆向きの運動によるコリオリ力が遠心力の2倍の大きさで内向きにはたらき, 遠心力とコリオリ力の合力が向心力となって逆向きの円運動が持続する」。
これを地球から見ると, 地球に乗ったものは止まったまま。
ということで, あたりまえだが, 並進座標系で考えたのと同じ運動になる。
もっとも, 実際には潮汐力があるので地球に乗ったもの (たとえば海水) の運動は円運動からずれるはずだが……
(注) 解説記事
「潮汐力は共通重心周りの遠心力で起こるのではない」
で, 天文学者である半田氏は潮汐力の教科書的説明を文字通りに解釈して, 公転運動に乗った回転系で, 月による重力と地球の公転運動による遠心力との合力を計算している。
その結果, 本来の潮汐力よりもずっと大きい奇妙な力 (じつは地球中心周りの遠心力……) が出てくるとして,
地球を逆方向に自転させて地球が慣性系に対して回転しないようにし, コリオリ力を計算に入れなければならないと主張している。
しかし回転系に乗ると遠心力が現れるのはあたりまえで, それを消そうとして地球を逆向きに回すのはナンセンスだ。
遠心力が出てくるのを避けたければ, 第4節のように慣性系で考えるか, 非回転系で考えればよいのだ。
じっさい, 半田氏は, 第6節では地球の自転を止めた非回転系で潮汐力を考えている。
ただし, 多くの解説記事と同じように地球を質点に分け, 各点の円運動を回転運動と勘違いし, 並進慣性力を遠心力と呼んでいる。
非回転系では遠心力が現れるはずがないのだが……。
残念ながら, これは誤解の多い解説記事だ。
第2部 潮汐
潮汐の位相についての誤解
つぎに, 現象としての潮汐について考えよう。地球の潮汐は, おもに月の潮汐力によって起こる。
(太陽による潮汐力も, 月の 0.46 倍ほどの大きさがあるが, ここでは考えないことにしよう。)
地球は公転に乗った回転系に対して24時間50分という短い周期で自転しているので, 地上の定点で見ると12時間25分ごとに満潮になる。
教科書には, その説明として, 月に近い側とその反対側の海面が膨らんだ地球の図が出てくる。
この図は, 海面の変形が十分速く, 潮汐力の変化に追いついて平衡状態になっていると仮定したときの図だ。
ところが, 現実には海面の変形は遅く, 教科書の図のようにはなっていない地点が多々ある。
たとえば西日本の太平洋岸では, 満潮の時刻は月の南中よりも6時間ほど遅れており, 月が南中するときには干潮になっている。
これは, 海洋の潮汐パターンが複雑で, たまたま西日本の太平洋岸では干満のタイミングが逆になっているだけなのだが, この点を捉えて教科書の説明は間違っていると主張する人をネット上でしばしば見かける。
その論理はつぎの通りだ。
地球に対する干満の位相の移動速度が 400 m/s もあるのに対して海洋を伝わる長波の速度は 200 m/s ぐらいしかない。
潮汐は外力による強制振動の問題で, 外力の変化が速すぎて応答できないときは, 強制振動の理論から振動の位相は外力より 180° 近く遅れるはずだ。
だから教科書の図は間違いで, いつも月と90° ずれた方向の海面が膨らんでいるはずだ。
西日本の太平洋岸の潮汐がその証拠だ, 等々。
潮汐を海水の強制振動の問題として扱うことは, 18世紀の Laplace の時代に遡る。
上記のにわか強制振動説が, これらの研究を踏まえたものとは思えない。
じっさい, 強制振動説は問題を単純化しすぎている。
なぜなら海洋の振動は, 質点ではなく波, つまり流体力学の問題として考えなければならないからだ。
波であれば, 波長が短くて周期が短い高調波が存在しうるので, ローカルには潮汐力の変化に追従した変形や共鳴が可能だ。
じっさい, 潮汐の位相は場所によってまちまちで, どこでも位相が 180° ずれているわけではない。
(ただし, 海洋潮汐と抵抗を伴う強制振動とのアナロジーはあるていど成り立つようだ。
後述のように, 地球全体で平均化すると, 海洋潮汐の位相と潮汐力の位相が大きくずれているのだ。)
実際の海洋は, 大陸によって分断された複雑な形をしており, 海の深さも場所によって異なる。
また, 地球が自転しているので, 海水は運動するとコリオリ力を受ける。このため, 海洋の振動はさらに複雑になる。
コリオリ力がはたらくときの波には, 通常の長波と同様の慣性波と呼ばれるモードの波のほか, 19世紀にケルビンが理論的に発見したケルビン波と呼ばれる波がある。
ケルビン波は, 岸で振幅が最大になるような波で, 北半球では岸を右に見る向きに伝わる。
たとえば北大西洋では潮汐力に共鳴したケルビン波が反時計まわりに回っている。
また, 水深が浅い各地の湾でも共鳴したケルビン波が回っている。
いっぽう太平洋は広すぎるので, いくつかの海盆ごとの波に分かれているようだ。
海洋潮汐の波のパターンは, 19世紀末には, 特定の周期をもついくつもの成分 (分潮という) に分けて解析されるようになった。
たとえば, 月による周期12時間25分の分潮は M2, 太陽による周期12時間ちょうどの分潮は S2,
地球の自転軸の傾きによる周期23時間56分の分潮は K1 と呼ばれる。
周波数が M2 と K1 の周波数の差に等しい, 周期25時間49分の O1 分潮も振幅が比較的大きい。
1990年代には, 衛星による潮位観測と数値計算に基づく海洋潮汐モデルが発展し, 分潮を合成することで潮汐をかなり正確に再現できるようになった。
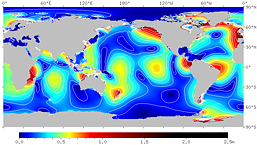
海洋潮汐モデルによる潮汐パターン (M2 分潮) を図13-図18に示す。
細かくて見えにくいが, 沿岸部には共鳴で潮差が大きくなっているところが多い。
このように, 海洋は複雑なパターンを描きながら, 自転に伴う潮汐力の変化に応答している。
図の作成には, 国立天文台の海洋潮汐モデル NAO.99b / NAO.99Jb
(国立天文台水沢) を使わせていただいた。
 |
 |
|
図13.月による潮汐 (M2 分潮) の振幅。
右は等高線つき。
|
 |
 |
|
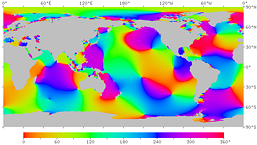
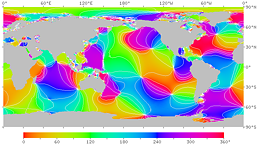
図14. 月による潮汐 (M2 分潮) の位相。
各点の満潮時刻 (GMT) を位相角で表す。右は等時線つき。
|
 |
 |
|
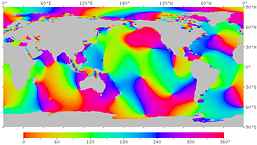
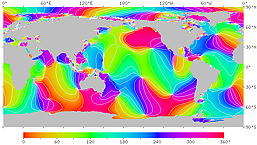
図14'. 月による潮汐 (M2 分潮) の位相の遅れ。 各点での月の南中から満潮までの時間 (月潮間隔) を位相角で表す。 360°は12時間25分にあたる。 右は等時線つき。
|
 |
 |
|
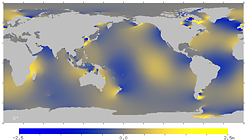
図15. 月による潮汐 (M2 分潮) のアニメーション。
白字の角度は, 位相角で表した時刻 (GMT)。
左は GIF アニメ, 右は手動アニメ。
|
 |
 |
|
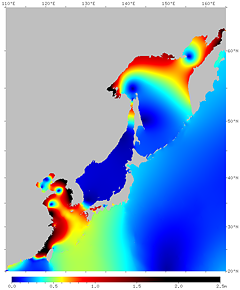
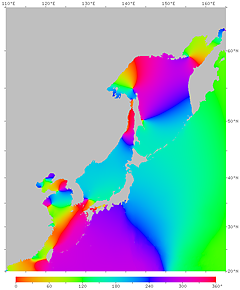
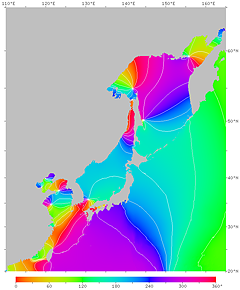
図16. 月による潮汐 (M2 分潮) の振幅。
|
 |
 |
|
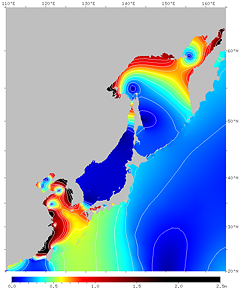
図17. 月による潮汐 (M2 分潮) の位相。
各点の満潮時刻 (GMT) を位相角で表す。
右は等高線つき。
月と位相が合っていたら 135°E での満潮時刻は −270° (約 −9 h) = +90°
になるはずだが, 実際には近畿地方の太平洋岸で約 260° になっている。
|
 |
 |
|
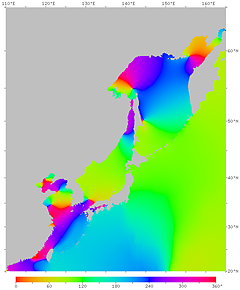
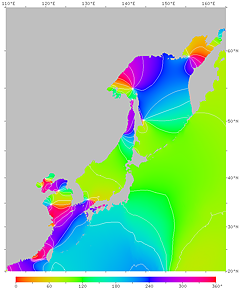
図17'. 月による潮汐 (M2 分潮) の位相の遅れ。
各点での月の南中から満潮までの時間 (月潮間隔) を位相角で表す。
360°は12時間25分にあたる。 右は等高線つき。
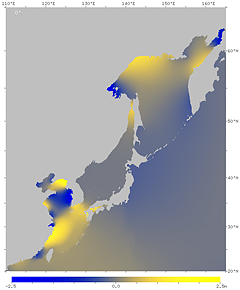
北海道・東北の太平洋岸で約 4 時間, 西日本の太平洋岸で約 6 時間, 岡山付近の瀬戸内海で約 11 時間の遅れがあることがわかる。
|
 |
 |
|
図18. 月による潮汐 (M2 分潮) のアニメーション。
白字の角度は,位相角で表した時刻 (GMT)。
左は GIF アニメ, 右は手動アニメ。
|
潮汐加速と潮汐ロック
図19は, 月による潮汐変形 (潮汐バルジ) の概念図だ。
実際には, 海洋潮汐のパターンは, 上で見てきたように, 各地で起こる共鳴のためにでこぼこしている。
潮汐の位相も場所によってまちまちだ。
このような複雑な潮汐パターンを平均化するために, 海洋潮汐モデルの M2 分潮を球面調和関数成分に分けると, 主成分の振幅 (潮差の半分) は筆者の計算では 9.6 cm になる。
(Wikipedia の "Tidal acceleration" には振幅は 3.23 cm と書いてあるが, これは3倍すると振幅になるように定義された係数を誤ってそのまま書いたものと思われる。)
また, 海洋潮汐 M2 分潮の球面調和関数主成分の向きは, 月の方向よりも角度で 65° ほど地球の自転の向きにずれている。
地上で見ると, 平均して月が南中から 65° 回ったころ (約4時間半後) に満潮がやってくることになる。
これは, 海洋の潮汐変形が海底との摩擦で地球の自転方向に引きずられるためだ。
摩擦には, 共鳴によって潮流が速くなる沿岸部の寄与が大きいということだ。
いっぽう, 固体地球も潮汐力によって変形している。
地球の硬さのため, 変形の大きさは潮汐力による平衡形状 (振幅 27 cm) の 0.6 倍程度 (振幅約 15 cm) にとどまっているが, それでもけっこう大きい。
固体地球の潮汐変形の向きも, 地球の内部摩擦のため月の方向から少しだけずれている。ただし, ずれはきわめて小さい (角度で 0.1° 程度) と見積もられている。
このほか, 固体地球は海洋潮汐による荷重変化のための二次的変形も受ける。上下変動の大きさは 1 cm 程度のようだ。
これらの, 固体地球の潮汐変形と海洋の潮汐変形を合わせた正味の潮汐変形は, 図19で示すように月の方向に対して角度で 3° ほどずれることになる。
よく見かける潮汐の説明図では, 固体地球は丸いままで海洋だけが変形しているように描かれている。
ところが, じつは固体地球の振幅は 15 cm ほど, 海洋の振幅は均すと 10 cm ほどなので, 固体地球の変形のほうが大きい。
また, 海洋潮汐は変形の向きも月の方向から大きくずれている。
ただし, 海水の密度が固体地球に比べて数分の1しかなく海洋潮汐の平均振幅も小さいため, 地球全体としての正味の潮汐変形のずれは 3° 程度だ。
 |
 |
|
図19. 海洋潮汐 (青) と固体地球潮汐 (茶色) を合わせた潮汐変形の向きは, 地球の自転に引きずられるため月の方向よりも少しずれている。
|
図19'. 観測によると, 海洋潮汐 (青) のずれの角度は約65°。
いっぽう, 地球潮汐 (茶色) のずれは約0.1°。
これらを合成したのが左図。
|
月による潮汐の影響は, 地球の変形だけではない。
地球を変形させた月自身も地球から大きい影響を受ける。 つまり, 図19のように変形した地球が, 月を進行方向に引っ張るのだ。
その結果, 月は地球から遠ざかり, そのぶん地球の自転は遅くなる。
潮汐加速と呼ばれる現象だ。
保存量である角運動量という語を使うと, 地球の自転角運動量が月の公転角運動量に移されるといえる。
月までの距離は, アポロが月面に置いてきた反射鏡にレーザー光線を当てることで測定できる。
また, 地球の自転周期は星の観測でわかる。
それによると, 月は世紀あたり3.8 mの速さで地球から遠ざかっている。
また地球の1日の長さは世紀あたり約2ミリ秒延びており, それが積もった時間のずれは (世紀)2 あたり約30秒になる (時間の2乗に比例する)。
図20は, 地球と月の角運動量の変化を, 月の軌道半径を横軸にして表したものだ。
潮汐加速の理論によると, 衛星の軌道半径は時間の平方の13乗根に比例する。
グラフに矢印で示した時間は, 潮汐加速のパラメータ (海洋の変化のしやすさや摩擦の大きさ) がつねに一定であるとして計算したものだ。
それによると, 500億年ほど先には地球の自転の周期が47日になって, 月の公転周期と同期することになる。
ところで, この図で使った過去45億年間で平均したパラメータに比べて, ここ何億年かの地球はずいぶん潮汐変形がしやすくなっているようだ。
というのも, 観測されている潮汐加速が, 過去の平均と比べて3倍も速いのだ。
大陸の移動による海洋の形の変化や自転周期が長くなってきたことが原因で海洋が潮汐力に共鳴しやすくなり, 摩擦が大きくなってきたのではないかと考えられている。
この調子でいくと地球の自転と月の公転の同期の時期はもっと早まるだろう。
さらに, 上の計算で無視した太陽による地球の自転の減速も効いてくる。
それでも, 太陽の寿命の前に同期が実現するのはむずかしいのではないだろうか。
 |
|
図20. 潮汐加速による月の軌道角運動量と軌道半径の関係。
曲線のそばの日数は地球の自転周期および月の公転周期。
矢印で示したのは月形成からの推定時間。
|
このように, 地球は質量が81分の1しかない月からいろいろ影響を受けている。
いっぽう, 月が地球から受ける潮汐力はずっと大きいので, その影響も甚大だ。
たとえば, 現在の軌道半径で月が地球から受ける潮汐力は, 月面での高さに換算すると地球方向で 13 m になる。
しかも, できたばかりの月は地球半径の数倍程度のところにいたと考えられている。
潮汐力は距離の3乗に反比例するので, 当時の月が受けていた潮汐力は今の千倍ほど, 高さに換算すると10 km以上はあったと思われる。
自転していた月は, 潮汐力を受けて大きく変形し, その変形した月は地球を引きずろうとして自転角運動量を急速に失う。
その結果, 月は短時間で自転できなくなる。
その時間は, 仮に月が地球半径の10倍ほどのところにあったとしても, わずか1000年ほどだ。
こうして, 潮汐変形した月は同じ側を地球に向けたまま回転系に固定される (図21)。
これを潮汐ロックまたは潮汐固定という。
これが, 月がいつも同じ側を地球に向けている原因だ。
潮汐ロックは, 固有の名前が付いた太陽系の主要な衛星で実現している。
固体の衛星では海をもつ地球と違って潮汐による自転減速の効率は悪いが, 親惑星の質量が大きく潮汐変形が激しいため, 短時間で潮汐ロックに至るのだ。
例外は, 土星の衛星ハイペリオン (衛星タイタンの軌道運動と共鳴してカオス的な自転をしている) や,
親惑星から遠く離れている土星の衛星フェーベ, 海王星の衛星ネレイド (どちらもまだ自転している) などだ。
いっぽう, 相対的に大きい衛星をもつ準惑星の冥王星では, 衛星カロンだけでなく, 冥王星本体もすでに潮汐ロック状態になっており, 相互ロックが実現している。
 |
|
図21. 太陽系の主要な衛星のほとんどは潮汐ロックされている。
|
つぎに, 潮汐ロック状態になった衛星の形について考えてみよう。
ロック状態の衛星は回転系に対して静止しているので, 回転系で考えるのが適切だ。
回転系では遠心力が現れるので, 衛星は潮汐力と遠心力の両方を受けることになる。
いま衛星を地球の月だとすると, 月の中心を原点としたポテンシャルエネルギーの式は, 式(14)で地球と月の立場を入れ替えるだけで得られる。
すなわち, 地球の重力によるポテンシャルを
\( V_{\rm{e}} \),
公転運動による遠心力ポテンシャルを
\( V_{\rm{c}} \) とすると
\[
\begin{eqnarray}
{V_{\rm{e}}} + {V_{\rm{c}}} &\approx& - \frac{{GM}}{{{a^3}}}({x^2} - {\textstyle{1 \over 2}}{y^2} -
{\textstyle{1 \over 2}}{z^2}) - \frac{1}{2}{\Omega ^2}({x^2} + {y^2}) + {\rm{const}}\\
&=& - \frac{{GM}}{{{a^3}}}({x^2} - {\textstyle{1 \over 2}}{y^2} - {\textstyle{1 \over 2}}{z^2}) -
\frac{1}{2}\frac{{G(M + m)}}{{{a^3}}}({x^2} + {y^2}) + {\rm{const}} . \tag{15}
\end{eqnarray}
\]
月の質量
\( m \)
が地球の質量
\( M \)
に比べてはるかに小さいとして
\( M+m \) の中の
\( m \) を無視すると, 上の式はつぎのようになる。
\[
{V_{\rm{e}}} + {V_{\rm{c}}} \approx - \frac{{GM}}{{{a^3}}}({x^2} - {\textstyle{1 \over 2}}{y^2} -
{\textstyle{1 \over 2}}{z^2}) - \frac{1}{2}\frac{{GM}}{{{a^3}}}({x^2} + {y^2}) + {\rm{const}} . \tag{16}
\]
第1項が地球による潮汐力, 第2項が月を中心とする遠心力だ。
式からわかるように, 衛星に対しては, 潮汐力と遠心力は同じオーダーの量になる。
 |
 |
 |
| 図22. 潮汐ロックされた衛星の潮汐力による変形 |
図23. 潮汐ロックされた衛星の遠心力による変形 |
図24. 潮汐ロックされた衛星の潮汐力+遠心力による変形 |
この式を微分して, 月面上での潮汐力と遠心力の大きさを求めると, x軸上とy軸上とz軸上での大きさは
\( (GMr)/{a^3} \) を単位として,
潮汐力が +2 : −1 : −1, 遠心力が 1 : 1: 0 となる。
ただし, \( r \) は月の半径だ。
これらの力による変形の大きさの比は, 潮汐力による変形が +2 : −1 : −1, 遠心力による変形が +1/3 : +1/3 : −2/3 となる (体積の変化が 0 になるように規格化してある)。
これらを加えると, x軸上, y軸上, z軸上での変形の大きさの比は +7/3 : −2/3 : −5/3 となる (図22~24参照)。
衛星が十分に柔らかであれば, この比で変形するはずだ。
実際には, どこかの段階で衛星は固化し, その後の軌道半径の変化と惑星から受ける力の変化によって徐々に変形するため, 理論どおりの形にはならないようだ。
(注. 上の議論では, ポテンシャルの形どおりに天体が変形するように書いた。
この描像が正しいのは, 質量が天体の中心に集中しているときだけだ。
実際には, 天体の変形でポテンシャルも変化するので, 変形は単純な計算よりも大きくなる。)
学校では, 月がいつも同じ側を地球に向けているのは月の自転周期と公転周期が一致しているからだと教えるが, それは同じ現象を別のことばで言いなおしているだけであって, 原因の説明にはなっていない。
ほんとうの原因は, 地球の潮汐力によって歪んだ力の場に月が「はまって」いるためだ。
学校教育では, 潮汐の話題のところで, 月も地球によって潮汐力を受けていることに触れてもよいのではないかと考える。
少なくとも教える側は潮汐ロックについて知っておいてほしいところだ。
(Roche 限界 2023年3月 追記)
潮汐加速に関連して, Roche 限界の説明をしておこう。
月のように, 衛星の公転周期が惑星の自転周期よりも長いと, 衛星は加速されて惑星から遠ざかる。
ところが, たとえば火星の Phobos のように, 衛星が惑星に近くて公転周期が惑星の自転周期よりも短いと, 衛星は減速されてますます惑星に近づくことになる。
そして, 衛星が惑星本体に近づきすぎると, 惑星による潮汐力が衛星自身の重力を上回り, 惑星に対して近い側と遠い側の岩がラピュタのように浮き上がって衛星が破壊されてしまうことになる。
このとき, 衛星が破壊されずにいられる限界の軌道半径を Roche 限界という。
ネットを見ていると, Roche 限界の計算を誤っているケースが多いので, ここで改めて説明しておきたい。
潮汐破壊が問題になるような, 衛星が惑星本体に接近している状況では, 衛星はすでに潮汐ロックされているはずだ。
したがって, 衛星に働く力は回転系に乗って考えなければならない。
すなわち, 衛星には潮汐力と遠心力の両方がはたらく。
衛星の質量
\( m \)
が惑星の質量
\( M \)
に比べてはるかに小さいとすると, 潮汐力ポテンシャルと遠心力ポテンシャルを足したものは 式(16) になる。
この式を \( x \) で微分すると,
\( x \) 方向の 潮汐力+遠心力 (単位質量あたり) を得ることができる。
衛星の半径を \( r \) とすると, 衛星表面での 潮汐力+遠心力 は,
\[
{F_x} = \frac{{3GM}}{{{a^3}}}r . \tag{17}
\]
いっぽう, 衛星表面での衛星自身の重力は,
\[
{F'_x} = - \frac{{Gm}}{{{r^2}}} . \tag{18}
\]
この2つの力がつり合う衛星の軌道半径 \( a \) が Roche 限界だ。
すなわち,
\[
a = {\left( {\frac{{3M}}{m}} \right)^{1/3}}r . \tag{19}
\]
ここで, 惑星や衛星の内部が一様であるとして, それぞれの密度を
\({\rho _{\text{M}}}\), \({\rho _{\text{m}}}\)
とする。 また, 惑星の半径を \( R \) とすると,
\(M = (4\pi /3){\rho _{\text{M}}}{R^3}\),
\(m = (4\pi /3){\rho _{\text{m}}}{r^3}\) なので, 式 (19) はつぎのように書くことができる。
\[
a = {\left( {\frac{{3{\rho _{\text{M}}}}}{{{\rho _{\text{m}}}}}} \right)^{1/3}}R
= 1.442{\left( {\frac{{{\rho _{\text{M}}}}}{{{\rho _{\text{m}}}}}} \right)^{1/3}}R . \tag{20}
\]
これは, 衛星が球形を保ったままで変形しないと仮定したときの Roche 限界なので, 剛体限界ということがある。
上式の括弧の中の係数が 3 ではなく 2 になっている解説をしばしば見かける (たとえば Wikipedia) が,
それは衛星が潮汐ロック状態にあることを忘れて遠心力を足してないからだ。
いっぽう, 衛星が液体のように自由に変形すると仮定すると, 衛星はポテンシャルに従って変形し, 細長くなって早い段階で壊れるようになるので, Roche 限界は上の式よりも大きくなる。
計算によると, このときの Roche 限界はつぎのようになる (天文学辞典)。
\[
a = 2.456{\left( {\frac{{{\rho _{\text{M}}}}}{{{\rho _{\text{m}}}}}} \right)^{1/3}}R. \tag{21}
\]
この Roche 限界を流体限界ということがある。
式 (21) の数値は衛星の密度が一様であると仮定したときのものだが, 衛星の密度は中心に近いほど高いのが現実的だ。
このようなとき, 衛星の平均密度を使って表した Roche 限界の値は, 式 (21) よりも少し小さくなるはずだ。
なお, 上の係数よりも少し小さい 2.423 という係数を使っている解説 (たとえば Wikipedia) があるが, それは衛星の形を単純な偏長回転楕円体と仮定して計算した近似値だ。
現実の衛星は, 流体のようにさらさらでもなければ剛体のように固くもないので, 流体限界と剛体限界の間のどこかの段階で破壊されることになる。
Phobos はすでに流体限界よりも内側にはいっており, 数千万年後には破壊されると予測されている。
環をもつ火星を見たいものだ。
第2部のおまけ
海洋潮汐がどれくらいでこぼこしているか知りたくて, 赤道付近の潮汐を描いたアニメーションを作ってみた。
計算には, 国立天文台の海洋潮汐モデルを使った。
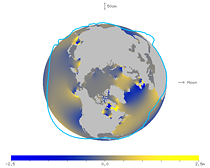
下の図は, 15°N から 15°S のあいだで平均した M2 分潮の潮位を強調して描いたものだ。
よく見ると, 月の方向から東に大きくずれたところで膨らむ傾向があることがわかる。
海洋と同じ縮尺で固体地球も上下に変形 (月の方向に +15 cm, 月と 90° 離れた方向に −15 cm) させておいた。
固体地球は水平方向にも少し変形するが, 図ではこれを無視した。
このように, 現実の潮汐変形は教科書に載っている説明図とはずいぶん違うようだ。
 |
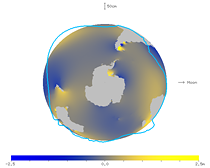 |
| 図25. 赤道付近の潮汐のアニメーション (北から見た図) |
図26. 赤道付近の潮汐のアニメーション (南から見た図) |
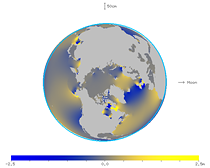
下の図は, 固体地球潮汐に乗せて海洋潮汐 M2 分潮の球面調和関数2次2階成分を描いたものだ。
海洋潮汐を平均化すると, 平均振幅約 10 cmの穏やかな成分が残る。
 |
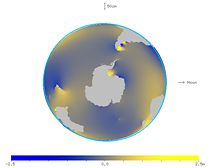 |
| 図27. 球面調和関数成分のアニメーション (北から見た図) |
図28. 球面調和関数成分のアニメーション (南から見た図) |
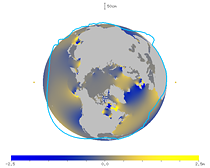
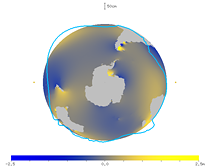
地球の自転に乗った回転系で見た潮汐のアニメーションも作ってみた。まずは M2 分潮の赤道付近での潮位の変化。小さい円 ● は月の方向とその反対の方向を表す。海洋がずいぶん遅れて応答していることがわかる。
 |
 |
| 図29. 赤道付近の潮汐のアニメーション (地球に乗って北から見た図) |
図30. 赤道付近の潮汐のアニメーション (地球に乗って南から見た図) |
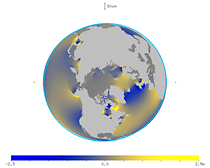
地球の自転に乗った回転系で見た潮汐を M2 分潮の球面調和関数2次2階成分で表したもの。
小さい円 ● は月の方向とその反対の方向を表す。
海洋の潮汐変形が 60°~70° ほど遅れていることがわかる。
 |
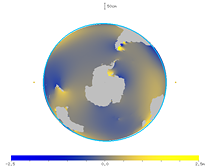 |
| 図31. 球面調和関数成分のアニメーション (地球に乗って北から見た図) |
図32. 球面調和関数成分のアニメーション (地球に乗って南から見た図) |
さいごに
本稿では, 潮汐力が重力の非一様性に起因する力であること, つまり地球の各点にはたらく重力と地球の中心にはたらく重力との差であることを示した。
地球の中心にはたらく重力との差をとる代わりに, その逆の力である並進慣性力を加えてもよい。
潮汐力をこのように合力で説明するばあい, 各点の重力と足す相手は並進慣性力であって, 回転系で現れる遠心力ではない。
じっさい, 回転系に乗って月の重力と共通重心の周りの遠心力の合力を計算しても, 潮汐力にはならない。
これは, 回転系で計算すると, 共通重心周りの遠心力の一部が地球を中心とする遠心力として潮汐力に加算されてしまうためだ。
つまり, 「重力と遠心力の合力」という説明は, そのままでは間違っている。
多くの教科書や解説記事をよく読むと,
「潮汐力を求めるときは地球の自転を止めて公転だけを考える。このとき, 公転による遠心力はどこでも大きさと向きが等しい」
と書いてある。
「公転による遠心力」は, 回転軸からの距離に比例するふつうの遠心力と違って, どこでも大きさと向きが等しい別種の遠心力だと主張したいようだ。
しかし, このとき地球は回転していない (向きを変えていない) ので, 地球に現れる慣性力は遠心力ではありえない。
じっさい, 剛体の力学で知られているように, この慣性力は並進加速度運動によって現れるふつうの一様な慣性力, すなわち並進慣性力だ。
2種類の遠心力があるわけではなく, 単に並進慣性力を遠心力の一種と思い込んでいるだけなのだ。
このように, 教科書や解説記事の多くは遠心力の定義を誤解している。
公転する地球に現れる慣性力が遠心力だと思っている人はおそらく, 地球が剛体であることを忘れて, 地球をたくさんの質点に分解し, 各点の円運動を各点の回転運動と勘違いしているのだろう。
剛体では, 円運動 (円に沿った並進運動) と回転運動 (向きを変える運動) は別の運動なので, 「回転」という語は注意深く使わなければならない。
すなわち, 自転を止めた地球の公転を「回転」と呼んではいけないし, 一様な慣性力を「遠心力」と呼んではいけない。
「回転」や「遠心力」の定義を勝手に変えてはならないのだ。
並進慣性力は, 回転系でも出てくる。
共通重心を中心としてまわる回転系に乗ると遠心力が現れるが, この遠心力を地球を中心とする遠心力と並進慣性力に分けることができるのだ
(一般に回転系では, 回転軸を共通重心から別の場所へ移すと, 遠心力のほかに並進慣性力が出てくる)。
潮汐力は, この並進慣性力と重力の合力として表すことができる。
この並進慣性力を, もとの遠心力の分力として出てきたからといって遠心力と呼んではいけない。
松田卓也氏は, 「間違いだらけの物理学」の中で, 並進慣性力のことを遠慮して「遠心力の一部の成分」と書いているが, はっきりと「慣性力」と書くべきであった
(「間違いだらけの物理学」4章 図11 の説明も, 遠心力ではなく慣性力と書くべきであった)。
学校教育における「遠心力」の誤用は, はるか昔から続いているのではないかと思われる。
というのも, ほとんどの潮汐の専門家が, 未だに並進慣性力のことを「大きさと向きが等しい遠心力」と呼んでいるからだ。
地球の自転を止めて考えているので, 地球に現れる慣性力が遠心力であるはずがない。
ところが, 潮汐の分野ではこの力のことを「大きさと向きが等しい遠心力」と呼んでもよいと思い込んでいるようだ。
その結果, 教育関係者は疑いもせずに並進慣性力を「遠心力」と呼ぶようになったのだろう。
潮汐の専門家にとっては, 用語を間違って使っていても, 計算は問題なくできるので不都合はないかもしれない。
しかし, 説明されたほうは「遠心力」と言われると回転系に現れる本来の遠心力と理解する。
まさか「遠心力」が並進慣性力の意味で使われているとは思わないだろう。
つまり, 地学で習う「遠心力」の意味が, 物理で習う本来の遠心力とは異なるのだ。
こうして, 教育現場での混乱が起きることになる
(教育現場だけでなく, 天文学者も混乱して誤った解説をしている……)。
「遠心力」の定義を分野によって勝手に拡張することは, 学問としても教育としても大問題だ。
潮汐力の説明に出てくる「遠心力」は早急に「慣性力」に改めるべきだ。
事実, 海外のサイトには, 「遠心力」ではなく「慣性力」を使って潮汐力を説明しているところがいくつかある (たとえば NOAA アメリカ海洋大気庁)。
「遠心力」が間違いであることに気付いている研究者や教育関係者は, 声を上げて教育機関や公的機関で続いている誤りを正していただきたい。
「慣性力」よりも「遠心力」で説明するほうが高校生にはわかりやすい, という現場の声があるかもしれないが, 間違いを教えてもよい言い訳にはならないだろう。
また, 遠心力がなぜ間違いなのかよくわからない人は, 物理の教科書 (たとえばランダウ-リフシッツ) を読んで剛体の力学を勉強しなおしてほしい。
では, 潮汐力をどう説明すればよいのか。
「潮汐力は, 地球の各点における月の重力と, 地球の中心にはたらく月の重力との差」
(たとえば 朝永振一郎編「物理学読本 第2版」1969 の 図 1-30)
は正しい説明なのだが, これだけではわかったような気がしないかもしれない。
「潮汐力は, 地球の各点にはたらく月の重力と, 地球が月に向かう加速度運動によって地球全体に一様にはたらく慣性力との合力。
重力と慣性力は, 地球の中心ではちょうど打ち消し合うが, 重力が場所によって異なるため地上の各点では打ち消し合わずに残る。」がよいと思うのだが, いかがだろう。
内容的には, 差をとる代わりに逆向きの力を足しただけなのだが。
ちなみにこれは, 自由落下するエレベータにはたらく潮汐力の説明と基本的に同じだ。
ウェブでは, 自由に発言ができることから気づかずに誤った自説を主張する人が多い。
たとえば, 多くの人が自由に参加している Wikipediaにも間違った記事が見受けられる。
英語ページは多くの人のチェックが入るのでまだ間違いが少ないが, 日本語ページには誤りが目立つ。
とくに潮汐力や潮汐は理解がむずかしいようで, 間違った記述が多い。
たとえば, 「潮汐力」の公転系での式では, 係数の 2 が抜けている。
また, 「潮汐」の遠心力の記述には, 地球の各点の円運動を回転運動と勘違いし, 各点に現れる並進慣性力を遠心力と誤解しているなど, 教科書と同様の間違いがある。
発言する人は, 自分の言説が正しいかどうか何か月もかけて考え抜いてほしいものである。
かくいう筆者も間違ったことを言っていないとは限らない。
本稿で述べたことについて, 筆者の誤解があればご指摘くださると幸甚である。
(「遠心力」のルーツは G.H. Darwin? 2021年7月 追記)
「大きさと向きが等しい遠心力」という表現のルーツを調べているうちに, George H. Darwin (Charles Darwin の息子) の
The tides and kindred phenomena in the solar system (1898) という19世紀末の本に行き着いた。
G.H. Darwin は月の潮汐加速理論を展開した天文学者で, 潮汐理論の大家でもある。
その Darwin が一般向けに書いたのが上の本だ。
よほど評判がよいのか, 100年以上経った今でも重版が続いている。
この本のなかで Darwin が潮汐力をわかりやすく説明するために採用したのが, 理想的なモデルとしての自転を止めた地球
(アイデアは Harvard 大学の W.M. Davis によるそうだ) と, その地球にはたらく「どこでも等しく平行な遠心力」だ。
一般の人にはわかりにくい「慣性力」の代わりに, 遠心力に似た力全般 (すなわち慣性力全般) の意味であえて「遠心力」という語を使ったのではないかと思われる。
しかし, 遠心力はあくまで回転軸からの距離に比例する力なので, 残念ながら並進慣性力を遠心力と呼ぶことはできない。
本当は「どこでも等しく平行な慣性力」と書くべきだった。
今でも重版が続いているという Darwin の知名度は驚異的だが, その知名度ゆえに「遠心力」の誤用が100年以上も続いているとしたら皮肉なことだ。
ところで, Darwin は Encyclopedia Britannica で Tides の項目を, 当時の最先端の話題まで含めて専門家向けに詳細に書いているが, そこでは潮汐力を「地球の中心にはたらく重力との差」と書いていて, 「遠心力」という語はいっさい使っていない。
このことから, Darwin は, 本来「慣性力」と書くべきところを, 誤用を承知で一般向けに「遠心力」と書いたのではないかと思われる。 本来の放射状の遠心力ではなく「どこでも等しく平行な」遠心力 (のような力) と断ることで, 「遠心力」を「慣性力」の代用として使ったのでは? というわけだ。
その「遠心力」が定着してしまい, 専門家も誤用であることに気付かず 100 年以上も使い続けている, というのが真相ではないだろうか。
( → G.H. Darwin 修正案 )
なお, 日本ではかつては「潮汐力は地球各点にはたらく重力と地球の中心にはたらく重力との差」と教えられていたようだ。
しかし, 現場の先生方が, なぜ月から遠い側でも満潮が起こるのか説明するのに苦労していたという。
そこで, 1960年代に Darwin 流の「どこでも同じ遠心力」が学校教育に導入され, 現場の先生方に歓迎されたそうだ。
そして, 公転による並進慣性力を遠心力と呼んでもよいという誤解が広がってしまった……。
アメリカでは, もう何年も前から潮汐力が inertial force を使って教えられている。
日本も, 一刻も早く誤解から脱却するべきだ。
リンク
- 松田 卓也, 猪坂 弘: 「潮汐力と潮汐」, 日本流体力学会年会 (2009)
- 松田 卓也: 「潮汐力と遠心力を巡るよくある誤解」, 基礎科学研究所 (2013)
- 松田 卓也: 「間違いだらけの物理学」, 学研出版 (2014)
- Matsuda,T., Isaka, H., and Boffin, H.M.J.: Confusion around the tidal force and the centrifugal force, Bulletin of JEin Institute for Fundamental Science (2015)
- 日本天文学会: 天文学辞典
- 国立天文台 RISE 月惑星探査プロジェクト: 「潮汐について」
… 補足1 の最後の「同じ大きさの遠心力」は「同じ大きさの慣性力」の間違い (後に改訂)。
また, 補足1にあるアニメーションは慣性系で見たものなので, 慣性力は現れないはずだ。慣性力は, 加速度系つまり地球に乗った座標系ではじめて見えるようになる。
- Feynman, R.: The Theory of Gravitation, The Feynman Lectures on Physics (1963)
… 図7-5の説明で "centrifugal force" を使ってしまったような。
- 国立天文台 水沢: NAO.99b 潮汐予測システム
… 海洋潮汐モデル nao99b.tar.gz と nao99Jb.tar.gz の M2 分潮のデータをアニメーションや振幅の計算に使わせていただいた。
- FNの高校物理: 動力学的潮汐理論におけるケルビン波
- 恒岡 美和: 「遠心力の取扱いについて」 物理教育 41, 38 (1993)
… 「遠心力」と「並進慣性力」の定義を説明し, 「遠心力」を乱用しないよう訴えている。
また, 慣性系における記述では「遠心力」を使ってはいけないことを指摘している。
- 斎藤 基彦: 「潮の満ち干」 (2007年6月, ほとんど同じ内容の「潮汐の話」が数理科学2012年6月号に掲載されている)
… 議論が明解でわかりやすい。「遠心力」を使った説明が誤りであることを指摘している。
また, 地球の自転軸の傾きによる1日周期の分潮についても述べている。
ロッシュ限界の計算で, 遠心力の寄与 (潮汐ロックされている衛星では遠心力を計算に入れないといけない) が抜け落ちているのが残念。
ロッシュ限界の公式 (剛体近似) に現れる係数は, 21/3 = 1.26 (Wikipedia も間違っている) ではなく 31/3 = 1.44 が正しい。
- Butikov, E.I.: The Physics of the Oceanic Tides (2017).
… 重力との合力の相手が遠心力ではなく地球の並進運動による一様な慣性力であることを指摘している。
- 朝永振一郎編 「物理学読本 [第2版]」 (1969)
… 潮汐力を, 地球各点での重力と地球中心での重力の差として, 正しく説明している
(参考: 図 1-30)。
- Ray, R.D.: A Global Ocean Tide Model From TOPEX/POSEIDON Altimetry: GOT99.2 (1999).
… 衛星観測による各分潮の球面調和関数成分の振幅, 位相 (PDF)。
Table 11 が M2 分潮の表。 振幅 D (単位 mm) が非正規化ルジャンドル陪関数の係数として定義されていることに注意。
- NOAA: National Ocean Service - Education (2005-)
… NOAA (アメリカ海洋大気庁) の教育サイトは "centrifugal force" ではなく "inertia" を使っている。
- Ross, D.A.: Introduction to Oceanography (1995).
… この海洋学の教科書では "centrifugal force" ではなく "inertial force" を使っている。
- Webb, P.: Introduction to Oceanography (2017).
… Roger Williams 大学が公開している海洋学の教科書も "inertia" を使っている。
- Taro's Page: 「朝日新聞『科学の扉』の潮汐の説明はおかしい」 (2017).
… 朝日新聞の解説記事や WEBRONZA の解説で潮汐力の説明に遠心力を使っているのはおかしいと指摘している。
じっさい, 並進慣性力を「遠心力」と呼んでいるかぎり, まともな解説は書けないだろう。
- 半田 利弘: 潮汐力は共通重心周りの遠心力で起こるのではない (2005).
… 公転に乗った回転系で重力と遠心力の合力を計算すると潮汐力が出てこないので, 回転系に対して地球を逆向きに自転させるなど, 混乱した内容になっている。 「回転」や「遠心力」の定義を誤解した, 間違いの多い解説記事なので要注意。
- 槙野 文命: 「潮汐力」のわかりやすい説明 (2010).
… 地球の公転運動を地球各点の円運動に分け, 円運動を回転運動と混同して並進慣性力を遠心力と呼ぶなど, 地学教科書と同じ間違いをしている。
また, 各点の円運動を拘束運動として説明している。 単なる剛体の並進運動なのだが……。
わかりやすい説明とは思えない。
- 谷村 省吾: 潮汐に関する誤解と正解 (2017).
… 松田氏と同様に, 潮汐力を回転系で説明する解説文。 並進慣性力を遠心力の平行成分などと紛らわしい名称で呼んだり遠心力と言い切ったりしている。 正しく「並進慣性力」と呼ぶべきだ。
- Darwin, G.H.: The tides and kindred phenomena in the solar system (1898).
… 潮汐理論の大家による一般向けの潮汐理論解説書。 「等しくて平行な遠心力 (equal and parallel centrifugal forces)」という表現が出てくる。
G.H. Darwin は, 一般にはあまり知られていない「慣性力」という語を避け, 代わりに「等しくて平行な」遠心力 (に似た力) という表現を使ったと推察される。
本当は「等しくて平行な慣性力」が正しい。
この本が, 遠心力を誤用した潮汐力の説明のルーツ?
100年以上も経つのにまだ重版が出ているという息の長い本。
Darwin Online,
Project Gutenberg
などで全文が読め, PDF でダウンロードすることもできる。
- Darwin, G.H.: "Tides", Encyclopedia Britannica (1902).
… 潮汐理論の大家による百科事典での専門的解説。 G.H. Darwin は, 専門家向けには潮汐力を地上各点での重力と地球中心での重力の差として説明しており, 「遠心力」をいっさい使っていない。
また, 海洋潮汐の強制振動モデル, 潮汐摩擦による地球の自転の減速と月の潮汐加速など, 当時の最先端の話題についても解説している。
- L.D.ランダウ, E.M.リフシッツ: 「力学・場の理論」 (ランダウ=リフシッツ理論物理学小教程 文庫版, 2008)
… 剛体の運動や遠心力については, この著名な解析力学・電磁気学の教科書の第6章 (とくに §24 と §29 *) に簡潔かつ正確に書かれている。
* 大教程「力学 第3版」(1976) では, 第6章 §31 と §39 にあたる。
これらの教科書の英語版は, PDF で公開されているのでダウンロードして読むことができる:
L.D. Landau, E.M. Lifshitz: Mechanics and Electrodynamics (1972),
L.D. Landau, E.M. Lifshitz:
Mechanics 3e (1976)
戻る
T. Fujiwara, last updated 2023/05
























