色空間の変換(1) - XYZ 色空間
CIE RGB 色空間と CIE XYZ 色空間
CIE が1931年に定めた CIE RGB と CIE XYZ について詳しく述べよう。このうち CIE XYZ
色空間は,いくつかの色空間を相互に変換するときの基本的な色空間として広く使われている。
色を RGB 3原色の混合で表すため,CIE は,まず3つの原色を単色光から選んだ。青と緑としては,入手しやすい水銀のスペクトル線 (図1)
の中から 435.8 nm の青い線と 546.1 nm の緑の線を使った。 また,赤としては,目が感じる光のうち事実上の長波長限界に近い
700 nm を選んだ。これらの3色を混合して作った色と任意の色を目で見て合わせるという等色実験 (図2参照)
を繰り返して,いろいろな波長の色を再現するための3成分の混合比を決め,得られたのが RGB 等色関数とよばれる曲線 (図3) だ。
図1. 水銀のスペクトルはいくつかの輝線でできている。数字は波長
(単位は nm)。
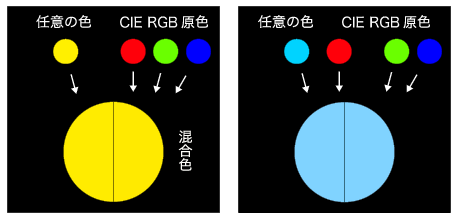 |
図2. 等色実験の概念図。混合色が,与えられた任意の色
(たとえば純色)
と同じ色に見えるように調整して混合比を求める。
任意の色が青緑系の純色のときは,彩度が高すぎて混合色では再現できず,任意の色側に赤を足して
(混合色から赤を引いて) はじめて同じ色になる。
このように,色によっては RGB の混合比のどれかが負になることがある。
|
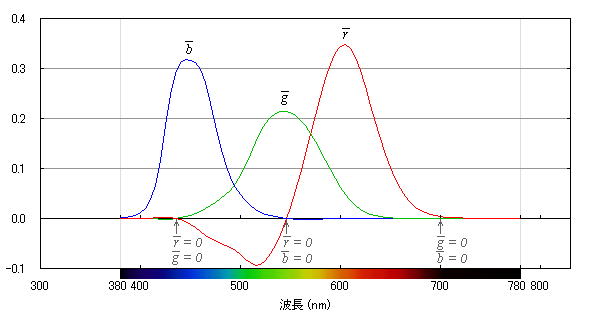
図3. CIE RGB 等色関数 (1931)。矢印の波長の色が3原色として使われた単色光。
この等色関数は,視野の中心部 (視野角 2°) の色覚をもとに1931年に決められたものだ
(1964年に視野角 10°の色覚から決められた等色関数もあるので注意)。図3をよく見ると,435.8 nm の色は B
だけの色なので,
r と g が 0
になっている。
同様に 546.1 nm では, r と b
が 0 になっている。
関数が負になっているところがあるが,これは,たとえば青緑の純色 (単色)
を3色の混合で作ろうとしても,青と緑で作った混合色の彩度が低すぎて,青緑の純色側に赤を足してやらないと同じ色にできないという意味だ。
なお,RGB 等色関数は,扱いやすいように,3つの曲線の下側の面積 (正しくは積分)
が等しくなるように調整されている。面積の計算に使う波長は,目が感じることができる範囲 380 nm ~ 780 nm と決めてある。
等色関数は,感度のようなもので,これに光のエネルギー分布をかけて積分すると,その色の R,
G, B 成分の値が求まる。
R, G, B
のままでもいいが,3成分のそれぞれの割合を小文字で r, g, b
と表すことが多い。すなわち
r = R/(R+G+B),
g = G/(R+G+B), b
= B/(R+G+B)
ここで r+g+b=1
なので,
b = 1−r−g
となる。すなわち r と g
がわかれば b は自動的に決まることになる。 R,
G, B の3成分からなる CIE RGB 色空間は3次元の空間であるが,明るさを無視した r と g からなる図 (色度図)
は平面で表現できるのでよく使われる。
色度図は,3次元での RGB の値を,原点を中心として
R+G+B = 一定
の面に投影し,座標軸が直交するように変形したものだ。 rg
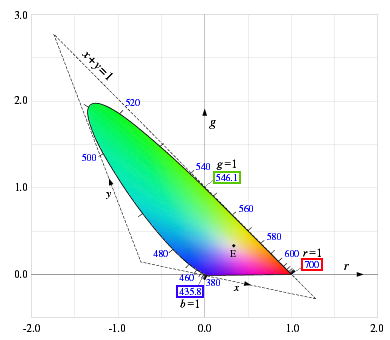
色度図にすべての色を描くと図4のようになる。外周の曲線は単色光の軌跡を表す。
緑から青にかけて r の値が負になるため,この部分が g
軸よりも左に大きくはみ出ていることがわかる。
また,波長 700 nm の光が r=1, g=0 に,
546.1 nm が r=0, g=1 に,
435.8 nm が r=0, g=0
にあたる。図の E 点は,エネルギー分布が一様 (フラット) な
E 光源の白色で,r=g=b = 1/3
になっている。
 |
 |
| 図4. rg 色度図 |
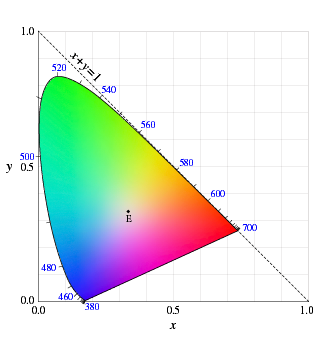
図5. xy 色度図 |
ところで,図3の RGB
等色関数は,値が負になったりするので,目の「感度」とするには感覚的に無理がある。また,負の値は数学的にも扱いにくい。
そこで,等色関数が負にならないように改良されたのが CIE XYZ 色空間だ。 XYZ の値は,RGB
から一次変換(後述)で得られるようにする。
X, Y, Z
の値をそのまま使う代わりに,全体に対する割合を小文字で表して使うことも多い。すなわち,
x = X/(X+Y+Z),
y = Y/(X+Y+Z), z
= Z/(X+Y+Z)
ここで x+y+z = 1
なので, z = 1−x−y
の関係がある。
ところで,XYZ の値が負にならないためには,新しい XYZ 色空間の座標軸のあいだにすべての色が収まるようにすればよい。すなわち,図4の
rg
色度図に破線で表したような三角形を作り,その2辺を XYZ の座標軸とすればよいことになる。
まず,等色実験から,CIE RGB の3原色を 1 : 4.5907 : 0.0601 の逆比で混合すると,ちょうど3つの色がつりあって白色
(E 光源の色, 後述)
と同じ色に見えることがわかった。
つまり,R, G, B がこの比で目の錐体の感度に寄与していると考えられる。
そこで,Y = 1R + 4.5907G + 0.0601B
と置いて,Y を明度を表す量とした。
図4の x 軸は,この Y
の値がちょうど 0 になる線である。
また,図4の x+y=1
の線は,色度図の赤の端での接線と一致するように選ぶ。
残る y 軸は,E光源に対して x=y=z=1/3
になることと,青緑の周辺で単色光の曲線が線の右側にぎりぎり収まることから決められる。このようにして CIE が決めた RGB から XYZ
への一次変換はつぎのようなものである。

|
X |

|
|
 |
0.49 |
0.31 |
0.20 |
 |
 |
R |
 |
|
 |
2.7689
|
1.7517 |
1.1302 |
 |
 |
R |
 |
| Y |
= 5.6508 |
0.17697
|
0.81240
|
0.01063 |
G |
=
|
1.0000 |
4.5907 |
0.0601 |
G |
| Z |
|
0.00 |
0.01 |
0.99 |
B |
|
0.0000 |
0.0565 |
5.5943 |
B |
この式で RGB 等色関数を変換すると,よく知られた XYZ 等色関数 (図6)
が得られる。関数の値はどこでも正または 0 になっている。また,すべての色について色度図を描くと図5 のような xy 色度図ができる。
これも,x≥0, y≥0, x+y≤1
の範囲に収まっていることがわかる。XYZ 色空間は,RGB
等色関数が負になってしまうという欠点を避けるために導入された,やや抽象的な色空間だ。X, Y, Z
が目の3種類の錐体細胞 (L,
M, S) の感度を表しているわけではない
(とくに Y は M錐体=緑 の感度ではなく,全色覚による「明度」に相当する)。
しかし,その後の研究でわかった錐体色素の吸収曲線は,この XYZ
等色関数とかなり似ている。XYZ 等色関数をヒトの錐体細胞の感度曲線を模したものと理解しても,全くの誤りというわけではなさそうだ。
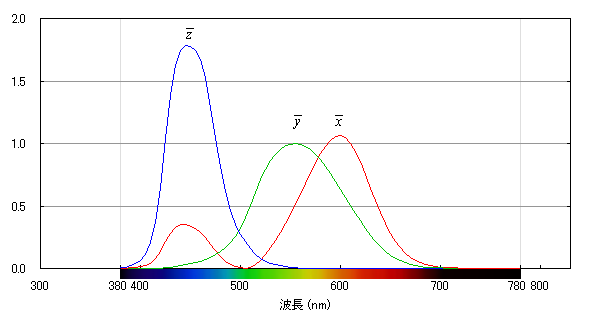
図6. CIE XYZ 等色関数 (1931)。380nm~780nmでの面積が等しくなるように定義されている。
光 (反射光または光源) のスペクトルが波長の関数として与えられたら,この XYZ 等色関数の x, y, z をそれぞれ掛けて波長で積分すると,色の3成分 XYZ が得られるわけだ。
すなわち,波長を λ, 光のスペクトルを P(λ) とすると,
X = ∫ P(λ) x(λ) dλ
Y = ∫ P(λ) y(λ) dλ
Z = ∫ P(λ) z(λ) dλ
(注) 「比視感度」は,視細胞の感度を表す曲線で,CIE
が数値化している。明るいところで錐体が感じる明るさを表す明所比視感度 (ピークは
555 nm) と,暗がりで桿体が感じる明るさを表す暗所比視感度 (ピークは 507 nm) がある。
等色関数の y
は明所比視感度に一致するように定義されている。
[文献]
https://www.rit.edu/cos/colorscience/rc_useful_data.php
… CIE 等色関数の数表 (Excel データ) などがある。
白色点
色を扱うときに重要になるのが,使う光源だ。われわれが見る色はふつう反射光なので,光源が変われば色も変わる。そこで,CIE
は標準光源としていくつかの光源を決めた。このうちよく使われるのが,図7に挙げたようなエネルギー分布を持つ光源だ。
これらは,白色系の光源を仮想化して数表として定義したもので,実在するわけではないが,似たような色の光源は存在する。
まず E は,エネルギー分布がフラットな光源で,CIE RGB, CIE XYZ の定義に使われた。また,C
は昼間の自然光を模した光源で,NTSC (アナログテレビの規格) の色の定義に使われた。D65 と D50
は,昼間の自然光のエネルギー分布により忠実に決められた光源で,それぞれ昼光色 (晴れた日の上方から来る光),昼白色
(晴れた日の地平線方向から来る光)
に相当する。数字の 65, 50 は,それぞれ色温度がほぼ 6500K,5000K であることを表している。
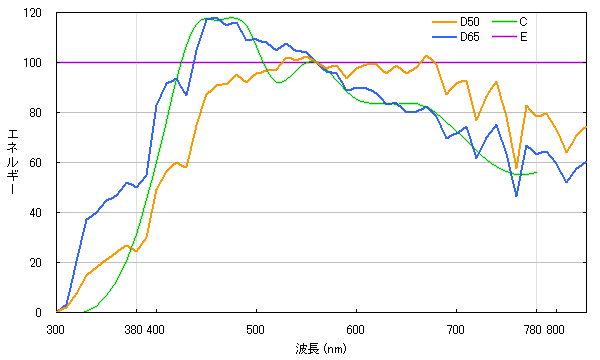
図7. おもな標準光源のエネルギー分布。波長 380nm~780nm が計算に使われる。
表1. 標準光源の白色点
| 標準光源 |
xw |
yw |
zw |
Xw |
Yw |
Zw |
備考 |
| E |
1/3 |
1/3 |
1/3 |
1.0 |
1.0
| 1.0 |
一様なエネルギー分布 (色温度 5454 K) |
| D50 |
0.345703 |
0.358539 |
0.295758 |
0.9642 |
1.0 |
0.8249 |
自然光を模擬 (昼白色, 色温度約 5000 K) |
| D65 |
0.3127 |
0.3290 |
0.3583 |
0.95046 |
1.0 |
1.08906 |
自然光を模擬 (昼光色, 色温度約 6500 K) |
| C |
0.31006 |
0.31616 |
0.37378 |
0.98071 |
1.0 |
1.18225 |
自然光を模擬 (色温度 6774 K, 古い規格) |
光源のエネルギー分布曲線が与えられたら,これに XYZ 等色関数をかけて積分することで「白」の3成分の値
Xw, Yw, Zw が決まる。
このとき,Yw=1 になるように数値を規格化 (normalize) する習慣がある。
表1に,いくつかの標準光源の白色点の座標を挙げた。小文字は,各成分の全体に対する割合で,xw+yw+zw
= 1 の関係がある。これらの白色点の座標は,色空間を変換するときに必要になる。
* D50 と D65 の定義については,それぞれ Xw,
Yw,
Zw を切りのいい数字にする流儀と,xw,
yw, zw
を切りのいい数値にする流儀があって,数値が微妙に異なることがある。ここでは,Adobe にならって,D50 は Xw,
Yw,
Zw をもとに,D65 は xw,
yw, zw をもとに定義した。
(注) 色温度
表面が黒い理想的な物体(黒体)を熱すると,熱放射を発する。この黒体放射のエネルギー分布 (プランク分布という)
は温度だけで決まり,その温度を色温度という。絶対温度 (セ氏温度に 273.15 を足したもの) で表される。単位は K
(ケルビン)。太陽の表面温度は約 6000 K なので,この前後の色温度は白く見える。色温度が低いと色は赤みを帯びる
(たとえば白熱電球の色温度は約 2900 K)。逆に色温度が高いと青白くなる
(XYZ 表色系 参照)。
色空間の変換 目次へ戻る
前へ 次へ
T.Fujiwara, 2011/12, 2019/09







