色空間の変換(3)  XYZ-Lab 変換


CIE XYZ から CIE Lab への変換

CIE Lab (以下 Lab) 空間では，色を L*, a*, b* の３つの数値で表す。Lab は，均質な色空間として色彩方面で広く使われている。Macintosh の ColorSync で，ディスプレイやプリンタの色域を表示するときの色空間としても使われている。ここでは，XYZ を Lab に変換することを考えよう。

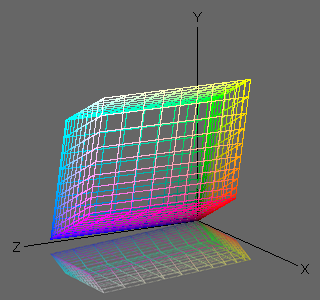
まず，標準光源だが，sRGB や Adobe RGB では D65 を使う。いっぽう，Lab では標準光源として D50 を使うことが多い (たとえば Photoshop の Lab は D50)。 標準光源が異なると反射光の色も変わってくるので，Lab に変換するためには，まず D65 を光源と仮定している sRGB や Adobe RGB の色 (XYZ 座標) を，D50 での色に直さなければならない。 これは，XYZ 空間でいえば，sRGB や Adobe RGB の色域の白色点を移動して平行六面体を変形することになる。 このような，光源の変更に伴う色の変化を近似的に実現する方法として Bradford 変換 という一次変換 (Photoshop でも使われている) を使うことにしよう。 図1と図2は，XYZ 空間での sRGB の色域 (D65 光源下) を Bradford 変換によって D50 光源下での色域に変換したものだ。 白色点が黄方向に少し移動しているのがわかるだろう。

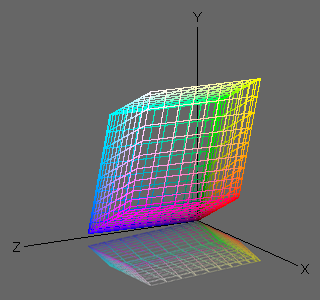sRGB (D65) gamut in the XYZ space sRGB (D50) gamut in the XYZ space
図1.  D65 光源下での sRGB 色域
 図2.  D50 光源下での sRGB の色域

 
RGB (D65) を XYZ に変換したあとで Bradford 変換を行う代わりに， ２つをまとめた変換をあらかじめ計算しておくと変換が一度で済む。 表1は，このようにして得られた変換行列だ。

表1. RGB(D65)→XYZ(D50) 変換行列
色空間
 M M －1
sRGB 
 0.436041  0.385113  0.143046
 0.222485  0.716905  0.060610
 0.013920  0.097067  0.713913
 
 3.134187 -1.617209 -0.490694
-0.978749  1.916130  0.033433
 0.071964 -0.228994  1.405754
P3-D65 
 0.515119  0.291978  0.157103
 0.241189  0.692244  0.066567
-0.001050  0.041879  0.784071
 
 2.403984 -0.989907 -0.397642
-0.842223  1.798844  0.016035
 0.048206 -0.097407  1.274005
Adobe RGB 
 0.609741  0.205273  0.149187
 0.311113  0.625675  0.063212
 0.019465  0.060874  0.744560
 
 1.962517 -0.610651 -0.341384
-0.978749  1.916130  0.033433
 0.028715 -0.140696  1.349266


さて，D50 光源下での XYZ が得られたら，Lab への変換だ。これは，(1) の関数 f (t)  を使って，以下の L*, a*, b* の式で求めることができる。 関数 f  の括弧の中の X, Y, Z の値がそれぞれ白色点の座標 Xw, Yw, Zw  で割ってあるのは，最大値を 1 に揃えるためだ。また，t が小さいところで f (t) が直線の式に切り替わっているのは，原点で f (t) のグラフの傾きが無限大になるのを避けるためだ。

f (t)  = { t 1/3 t > (6/29)3 = 0.008856... のとき
[(29/3)3 t + 16] /116      
上記以外
(1)

L* = 116 f (Y/Yw) − 16
a* = 500 [ f (X/Xw) − f (Y/Yw)]
b* = 200 [ f (Y/Yw) − f (Z/Zw)]


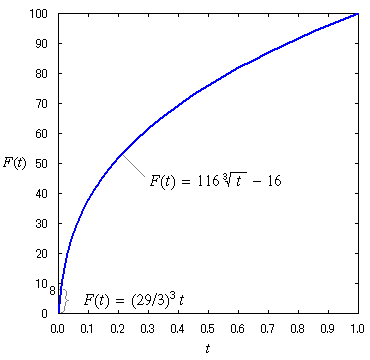
L*, a*, b* の式には上の(1)の f (t) を使って定義するのが一般的だが，つぎの(2)のような F(t) を使って表すほうがわかりやすいかもしれない。

F(t)  = { 116 t 1/3 − 16         
t > (6/29)3 = 0.008856... のとき
(29/3)3 t
 上記以外
(2)

この F を使うと，L*, a*, b* はつぎのように表すことができる。

L* =  F(Y/Yw)
a* = (500/116) [F(X/Xw) − F(Y/Yw)]
b* = (200/116) [F(Y/Yw) − F(Z/Zw)]


nonlinear function for the XYZ-Lab conversion
図3. XYZ→Lab 変換で使われる非線形の関数

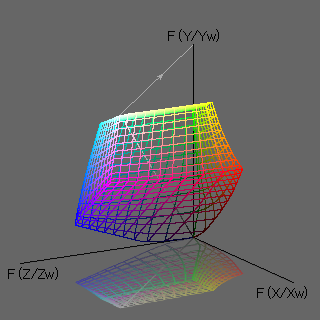
 F(t) は，目の感覚が直線的ではない (明るさに比例しない, Weber–Fechner の法則) ことを模擬した式で，グラフで表すと図3のような曲線になる。 まず，この F を使って X, Y, Z それぞれの明るさを目の感覚に近くなるように変換しておく。図4は，この時点での sRGB の色域を表したものだ。 F による変換で X, Y, Z それぞれの中間の階調が明るくなるため，図2で平行六面体だった sRGB の色域が，図4ではかなり歪んでいることがわかる。
この F を使って Y の値 (比視感度) を変換したもの，すなわち図4での XZ 平面からの高さが L* (明度) だ。また，X/Xw=Y/Yw=Z/Zw とおくと a*=0, b*=0 となることからわかるように，図4の原点から白色点に向かう無彩色の直線が Lab 空間での L* 軸になる。この無彩色直線からの X 軸の正方向および Z 軸の負方向への色差をそれぞれ何倍かしたものが a* および b* だ。こうしてできたのが，図5の Lab 色空間だ。 L*, a*, b* それぞれの軸方向の倍率が異なるのは，色空間ができるだけ均質になるように調整した結果だ。

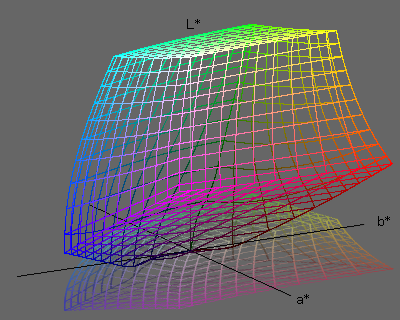sRGB gamut in F(X/Xn), F(Y/Yn), F(Z/Zn) space sRGB gamut in the Lab space
図4. 関数 F に従って X, Y, Z を変換する
 図5. 無彩色の軸を図4の矢印のように移動し，X方向，Z方向にそれぞれ拡大すると Lab になる


(参考) RGB → Lab 変換を，別のアングルから見た一連の図 でも示したおいた。

(参考) L* の 値は 0～100 に限られるが，a*, b* の絶対値は色によっては 100 を越えることもある。sRGB, P3-D65 (Display P3), Adobe RGB, 最適色立体(物理的に可能な反射光すべて) それぞれの色域を Lab 色空間で立体的に表したもの (アニメーション) を以下に置いておくので，参考にしてほしい。
　

CIE Lab → CIE XYZ 変換

Lab 色空間から XYZ の値に戻すには，(1) または (2) の逆の変換を行えばよい。すなわち

 fy = (L*+16) / 116
 fx =  fy + (a*/500)
 fz =  fy − (b*/200)
とすると
Y =  fy3Yw    ( fy > 6/29 のとき) ，または    Y = (3/29)3 (116 fy − 16) Yw      ( fy ≤ 6/29 のとき)
X =  fx3Xw    ( fx > 6/29 のとき) ，または    X = (3/29)3 (116 fx − 16) Xw      ( fx ≤ 6/29 のとき)
Z =  fz3Zw   ( fz > 6/29 のとき) ，または    Z = (3/29)3 (116 fz − 16) Zw       ( fz ≤ 6/29 のとき)

で XYZ が得られる。 Lab の標準光源が D50 であれば，この逆変換で得られた XYZ は D50 光源の下でのものだ。したがって，XYZ を RGB (sRGB や Adobe RGB) に変換するときは，表(2)の逆行列を使わなければならない。こうして得られた RGB にさらに明るさの補正（ガンマ補正）を行うと，sRGB / Adobe RGB の RGB データ R', G', B' になる。


色空間の変換 目次へ戻る   前へ 次へ
T. Fujiwara, 2011/12, 2019/09